In this article, we will look at the acceleration formula with mass and force. We already have discussed the acceleration formula with velocity and time. In this article, we will look at the formula for acceleration with mass and force. We use the acceleration formula with mass and force when we do not have any knowledge of the velocity of the moving body and time. In this case, we only have information about
- Force (f) acting on the body or object and
- Mass (m) of the body or object
According to Newton’s second law of motion, force is mass times acceleration we can use this relation to find the acceleration of the moving object. Of course, we need to have force acting and mass.
Acceleration formula with mass and force
We know that the force formula according to Newton’s second law of motion is \[f=m\times a\] Now if we want to find acceleration from this force formula then we would have to rearrange the above equation. So, rearranging above equation we get \[a=\frac{f}{m}\] Here,
- acceleration \(a\) is in \(m/s^2\)
- force \(f\) is in N (or \(Kg.m/sec^2\))
- mass \(m\) is in \(Kg\)
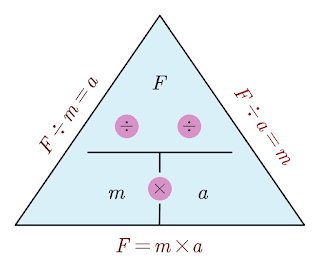
We can also use the force formula triangle to find the third quantity if any two of force, mass, and acceleration are given.
Solved questions based on acceleration formula with mass and force
Question 1 A car of mass 1000 Kg is moving with velocity 10 m/s and is acted upon by a forward force of 1000 N due to engine and a retarding force of 500N due to friction. What will be its velocity after 10 seconds?
Solution Here it is given that\(m=1000 Kg\)\(u=10ms^{-1}\)\(t=10 s\)We have to find velocity \(v\) after 10 seconds.Net forward force,
\(F= \text{Forward force} – \text{Retarding force}\)
\(F=1000 N-500 N=500 N\)
Acceleration
\(a=\frac{F}{m}=\frac{500}{1000}=\frac{}{2}ms^{-2}\)
From kinematic equation of uniformly accelerated motion\(v=u+at\)
So we have
\(v=10+\frac{1}{2}\times 10 = 15 ms^{-1}\)
Question 2 A force of 72 dynes is inclined to the horizontal at an angle of \(60^{\circ}\). Find the acceleration in the mass of \(9g\), which moves in a horizontal direction.
Solution Here it is given in the question that
\(m=9g\), \(F=72 dyne\), \(\theta=60^0\)
The horizontal component of the force is
\(F_x=F\cos \theta= 72 \times \cos 60^0 \)
\(F_x=72\times .5=36 dynes\)
Acceleration,
\(a=\frac{F_x}{m} = \frac{36}{9}=4 cm.s^{-2}\)
Further Reading