Constant negative velocity graph

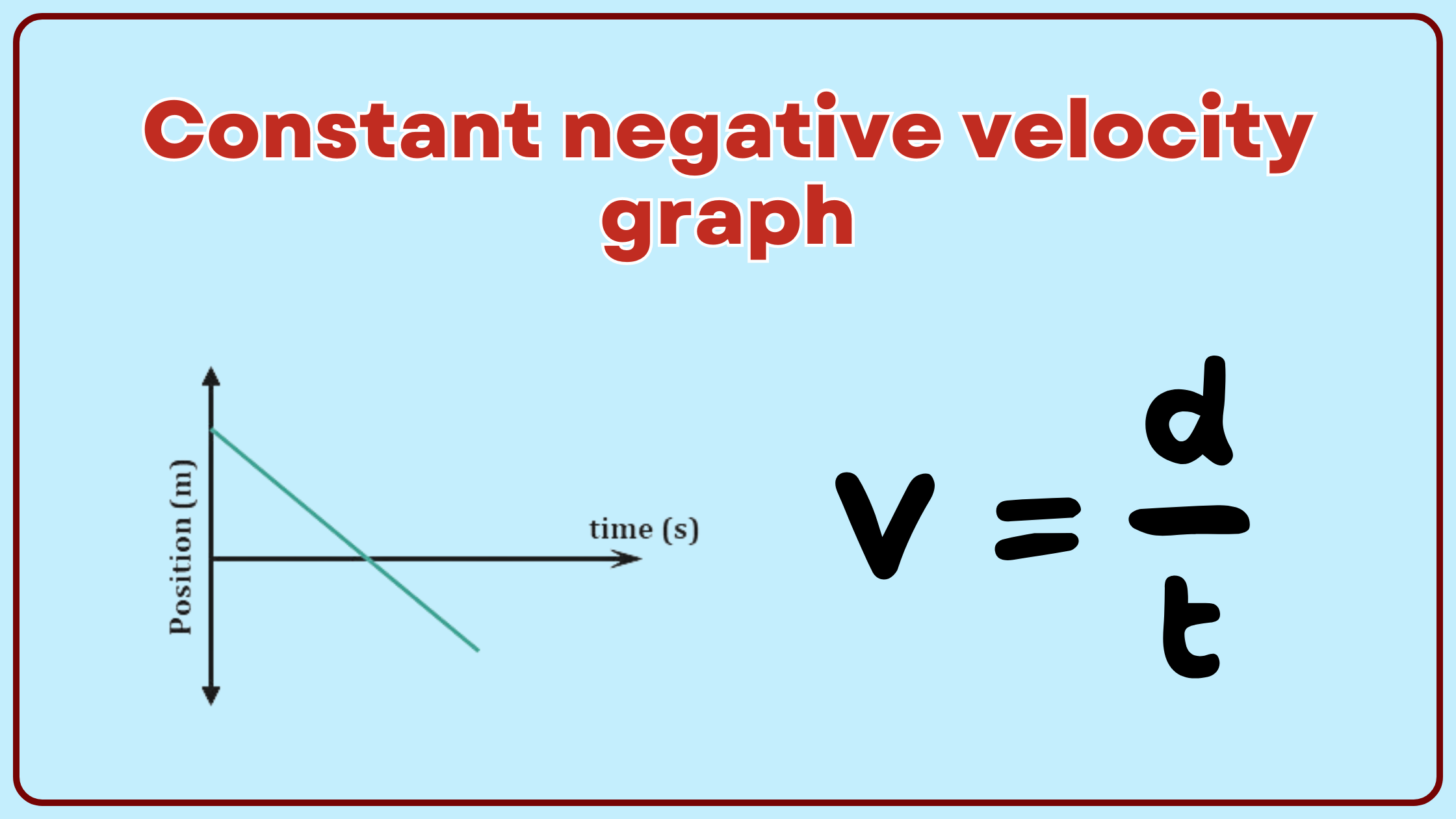
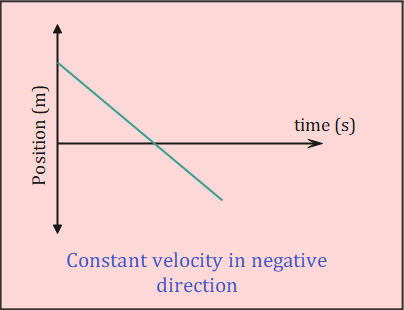
A constant negative velocity graph is a straight line with a negative slope on a position-time graph, representing an object moving at a constant speed in the opposite direction of the positive axis.

Explanation

In physics, velocity is a vector quantity that describes both the speed and direction of an object’s motion. When we talk about a constant negative velocity, we’re referring to an object moving at a steady speed in a direction opposite to what we’ve defined as positive.

On a position-time graph, this motion appears as a straight line sloping downward from left to right. The steepness of this line indicates the magnitude of the velocity – a steeper line means a faster speed.

Key Features of a Constant Negative Velocity Graph:

1. Straight Line: The graph is always a straight line, indicating that the velocity doesn’t change over time.
2. Negative Slope: The line slopes downward from left to right, showing that the position is decreasing over time.
3. Constant Slope: The slope of the line remains the same throughout, representing a constant velocity.

Mathematical Representation

The equation for a straight line on a position-time graph is:

$$ x = x_0 + vt $$

Where:

• $x$ is the position at time $t$
• $x_0$ is the initial position
• $v$ is the velocity
• $t$ is the time

For a constant negative velocity, $v$ would be a negative value.

The slope of this line represents the velocity:

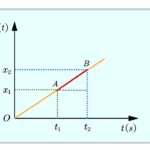
$$ v = \frac{\Delta x}{\Delta t} = \frac{x_2 – x_1}{t_2 – t_1} $$

For a constant negative velocity, this slope will be negative and constant throughout the motion.

Real-World Examples

Constant negative velocity can be observed in various scenarios:

1. A car reversing at a steady speed
2. An elevator descending at a constant rate
3. A submarine diving at a uniform speed

Importance in Physics

Understanding constant negative velocity graphs is crucial for:

1. Interpreting motion in one dimension
2. Calculating displacement and average velocity
3. Comparing different types of motion
4. Solving problems involving uniform motion

By analyzing these graphs, students can gain insights into an object’s position, direction of motion, and speed at any given time. This forms a foundation for more complex concepts in kinematics and dynamics.

Remember, the “negative” in constant negative velocity doesn’t imply slowing down – it simply indicates motion in the opposite direction to what we’ve defined as positive. The object is still moving at a constant speed, just in the reverse direction.