In this article we will learn about the comparison between Coulomb’s laws and Biot-Savart’s laws. We will look at both similarities and difference between Coulomb’s Law and Biot-Savart’s law. One is for static charges and another one is for moving charges. However both the forces explained by these laws are of electric origin. Coulomb’s Law is which gives electric force between charges can be used to define Electrostatic Field and Biot-Savart’s Law defines the Magnetic Field due to a current carrying wire.
What is Coulomb’s Law
This law of electrostatics explains how static charges interact with each other and on what factors the forces between them depends. According to this Law
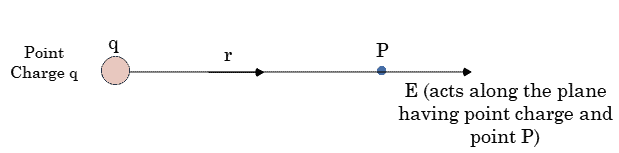
Electric force between two charges $q_1$ and $q_2$ kep at distance $r$
- is directly proportional to product of two charges $F \propto {q_1}{q_2}$
- is inversely proportional to square of distance between two charges $F \propto \frac{1}{r^2}$
- $F = k\frac{{{q_1}{q_2}}}{{{r^2}}}$ where, where, $k$ is the constant of proportionality. The value of $k=8.85 \times 10^{−12}C^2/Nm^2$ in vacuum
What is Biot-Savart’s Law
A conductor carrying current I produces a magnetic field around it. Biot-Savart law gives us expression for the magnetic field at a point due to a current element
According to this law, the magnitude dB of magnetic field at point P due to the current element depends upon the following factors
- $dB\propto I$
- $dB\propto dl$
- $dB\propto \frac{1}{r^2}$
- $dB\propto \sin\theta$
Mathematically,
$dB=\frac{\mu_0}{4\pi}\cdot\frac{Idl\sin\theta}{r^2}$
above equation gives the magnitude of the magnetic field at a point due to small current element $Id\vec{l}$. The electric currents element is a vector quantity. It must be noted that this law holds strictly for steady current only.

The similarity between Coulomb’s law and Biot-Savart’s Law
- Both the electric and magnetic field depends inversely on the square of the distance between the field source and field points in question.
- Both of them are long-range forces.
- Both of them obey the Superposition Principle.
Differences between Coulomb’s law and Biot-Savart’s Law
- The electric charge element $dq$ producing electrostatic field is a scalar source whereas the electric current element producing magnetic field $Id\vec{l}$ is a vector source having direction same as that of the flow of current.
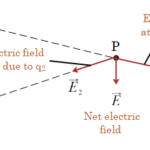
- Electric field $E$ acts along the displacement vector whereas $B$ acts perpendicular to $dl\times r$. According to Coulomb’s law, the magnitude of the electric field at any point (P) depends only on the distance of the charge element from any point (P). According to Biot-Savart’s law, the direction of the magnetic field is perpendicular to the current element as well as to the line joining the current element to the point P.
- Electric field $(E)$ is not dependent on angle whereas the magnetic field $(B)$ depends upon angle $(\theta)$ where $(\theta)$ is the angle between $(v)$ (the velocity of moving charge) and $(B)$ (the magnetic field).
Comparison in tabular form
| Biot-Savart’s Law for Magnetic Field | Coulomb’s Law for electrostatic Field |
|---|---|
| Long Range Force | Long Range Force |
| Principle of superposition applies | Principle of superposition applies |
| Field is produced by vector source $Id\vec{l}$ | Field is produced by electric charge that is scalar |
| There is an angle dependence in the Biot-Savart’s Law | There is no angle dependence in Coulomb’s Law |
| The magnetic field acts perpendicular to the plane containing the current element $Id\vec{l}$ and displacement vector $\vec{r}$ which is along the direction of their cross product. | The electrostatic force or field acts along line joining source and the point. |
Related Article