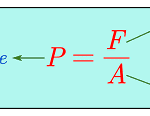Dimensions of stress are: [PMT/NEET-2020]
a. $[ML^{-1}T^{-2}]$
b. $[MLT^{-2}]$
c. $[ML^{2}T^{-2}]$
d. $[M L^{0}T^{-2}]$

Answer: a. $ [ML^{-1}T^{-2}] $

Explanation:
Stress is defined as the force applied per unit area of a material.

$ \text{Stress} = \frac{\text{Force}}{\text{Area}} $

Dimensional Analysis

• Force has dimensions: $ [MLT^{-2}] $
  (From Newton’s second law $ F = ma $)
• Area has dimensions: $ [L^{2}] $
  (Area = length × width)
• Therefore, stress has dimensions:
  $ \frac{[MLT^{-2}]}{[L^{2}]} = [ML^{1-2}T^{-2}] = [ML^{-1}T^{-2}] $

Physical Understanding

The dimension $ [ML^{-1}T^{-2}] $ represents pressure-like quantities. This makes physical sense because:

• Stress measures the internal forces within a material
• It has the same dimensions as pressure, which is also force per unit area
• Higher stress means more force concentrated over a smaller area

Examples of Stress

Common types of stress include:

• Tensile stress (pulling forces)
• Compressive stress (pushing forces)
• Shear stress (forces parallel to the surface)

All these types of stress share the same dimensional formula $ [ML^{-1}T^{-2}] $, confirming our answer.