A frequent type of motion that almost everyone observes daily is freefall. When we drop something from a certain height, we can easily observe its motion.
For many years in the past, many thinkers and scientists believed that the speed with which something fell was determined by its mass. This idea seems to be natural and logical. However, in the 16th century, Galileo had suspected that all objects fell with the same acceleration, despite the difference in their mass. If he dropped two objects, one light and one heavy, from a great height, they would both hit the earth at the same time. This established that acceleration due to gravity is mass independent.
What is free fall?
When an object is thrown down from a certain height, it will have a slow start or less speed, to begin with. As it continues to fall, it gains speed until it achieves its maximum speed before hitting the ground. Numerous elements influence the speed of an object in free-fall motion.
Freefall is a term used in physics to describe an object falling under its weight. It is also known as free-fall because nothing is holding the object down. The object falls freely until it hits the ground.
Freefall is described in Newtonian physics as the motion of an object where gravity is the sole force acting on it.
Conditions for free fall motion
There are two important conditions we must remember for free-falling objects:
- Air resistance does not exist for free-falling objects.
- On Earth, all free-falling objects accelerate at $9.8 m/s^2$ (commonly estimated as $10 m/s^2$ for calculation purposes).
Here, in the first condition, we are assuming the absence of air resistance for free-falling objects. This means the motion is in a vacuum. Viscous force or thrust of the medium has no effect on the motion. This condition is only an approximation made for ease of calculation. In reality, there is always a force of air resistance present in the environment. We will hold on to this assumption while solving problems related to free-fall motion until and unless it is stated otherwise in the problem.
The second condition talks about the constant acceleration. When an object falls, it experiences a force called gravity. Gravity pulls the object towards Earth’s center with the same constant acceleration irrespective of whether it is a light object or a heavy object.
Free Fall Motion is a special case
Freefall is a special case where the acceleration due to gravity is constant and acts in the downward direction. The term “freely falling object” does not always refer to an object that has been dropped from its state of rest. This is true even if the object is thrown upwards or has no velocity.
Some misconceptions about free fall motion
Some people believe that the final velocity of a freely falling object under gravity is zero since the object comes to rest when it reaches the ground, but this is not true. In physics questions, the final velocity is defined as the speed at which the object touches the ground right before it stops. Once the object makes contact with the ground, it ceases to be in free fall.
Free Fall Motion Examples
Some of the examples of free-fall motion are given as follows
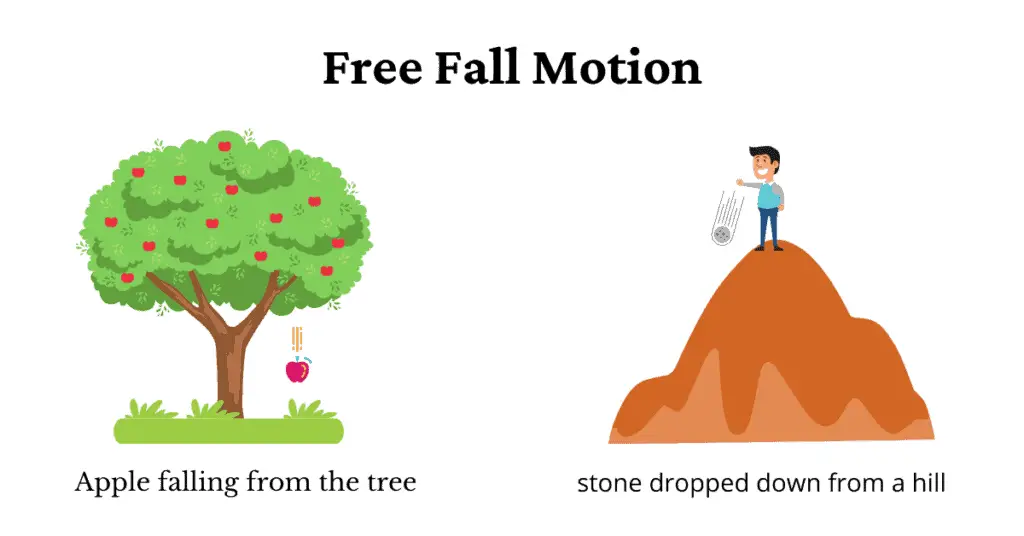
1. A stone dropped down from a hill.
2. Apple falling from a tree.
3. An object on its way down in projectile motion.
4. Raindrops falling from the clouds to the ground, or hail falling with the rain.
5. A ball thrown upward comes down to earth in a free fall.
Equations Of Motion For Freely Falling Object
We already know about kinematic equations of motion for a uniform acceleration and they are given by relations
$$v = {v_0} + at$$ $$x = {x_0} + {v_0}t + {1 \over 2}a{t^2}$$ $${v^2} = {v_0}^2 + 2a(x – {x_0})$$ $$\overline v = {1 \over 2}(v + {v_0})$$
These equations of motion can be applied to free-fall motion since it is the motion of objects falling under the influence of gravity and we already know that acceleration due to gravity $g=9.8m/s^2$
Since the acceleration due to gravity for freely falling bodies is denoted by the letter $g$, we replace the acceleration $a$ of the equations with $g$, and since the vertical distance of freely falling bodies is known as height $h$, we replace the distance $s$ in our equations with the height $h$.
$$v = {v_0} + gt$$ $$h = {v_0}t + {1 \over 2}g{t^2}$$ $${v^2} = {v_0}^2 + 2gh$$
These revised equations can be used to solve numerical problems. Before we do so, it’s crucial to remember the following points about the motion of freely falling objects.
- When a body is dropped from a certain height $h$, its initial velocity, $v_0$ is zero.
- The final velocity $v$ of an object thrown vertically upwards is zero.
- The time it takes for the body to reach its highest peak is the same as the time it takes to fall down from the same height.
Solved Problems
Question 1: A person throws a ball vertically upward with an initial velocity of $15m/s^2$. Calculate (i) How high it goes (ii) How long the ball is in the air before it comes back to his hands.
Solution: First of all we will fix our origin on the surface of the earth or ground. The upward displacement and velocity will be positive and the downward displacement and velocity will be negative. Acceleration due to gravity $g=9.8m/s^2$ always acts in a downwards direction.
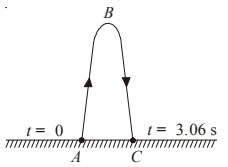
(i) At the highest point, velocity is zero.
Now, $${v^2} – {v_0}^2 = 2gh$$
Here, $v=0$ : $v_0=+15m/s$ : $g=-9.8m/s^2$
Therefore
$(0)^2-(+15)^2=2\times (-9.8) \times h$
Therefor maximum height is
$h=\frac{-(+15)^2}{2\times (-9.8)}=11.5 m$
(ii) We know that
$h=v_0t+\frac{1}{2}gt^2$
Since the net displacement of the journey is zero. So, here
$h=0$ , $v_0=+15m/s$ , $g=-9.8m/s^2$
$0=15t-\frac{1}{2}\times 9.8t^2$
or,
$0=15t-4.9t^2$
Therefore,
$0=t(15-4.9t)$
this gives
$t=0$ and
$15-4.9t=0$
or,
$t=\frac{15}{4.9}=3.06s$
You must have noted that there are two solutions for $t$; 0 s and 3.06 s. The first solution corresponds to initial point A and the second solution corresponds to return point C. Therefore the ball is in the air for 3.06 s.
Free Fall Motion Quiz
Choose the correct option from the single choice type questions given below. You can finish the quiz by using the View Results button at any time.