In this article learn about how to find displacement in physics. Here we will learn about Displacement formulas and how to use them to find displacement in physics.
Many people use the terms distance and displacement interchangeably. But in reality, both distance and displacement are two different concepts.
Displacement is defined as a change in the position of an object. Now when an object is displaced it covers a distance in a particular direction.
Since it has both magnitude and direction displacement is a vector quantity. For more clarity consider an object moving from point A to point B.
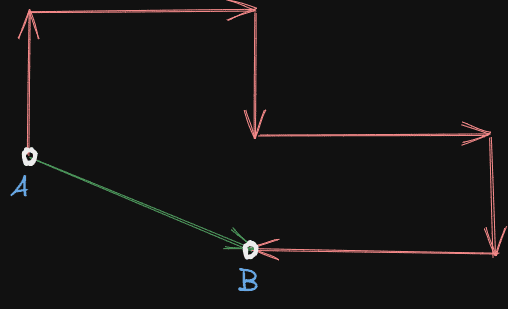
Here the object under consideration moves through this red line path. Here this red line’s path gives the total distance covered by the object moving from point A to point B.
But the green line points from point A to point B in the shortest possible distance between these two points with its direction pointing from initial point A to final point B. This shortest distance from point A to point B is nothing but a displacement of the object.
Now as such we have two cases of formulas for finding displacement in kinematics.
- The first one is where only the position of the object is given that is we have information about the initial and final positions of the object in motion.
- In our second case, we use kinematics equations that involve distance along with other parameters like velocity, acceleration, and time.
However, in this article, we would only find the displacement of the object without involving other kinematics quantities like velocity, acceleration, and time. So, here we will learn how to find displacement without time.
Let us now look at how to find displacement in physics.
The formula for displacement in physics
If we have knowledge about the initial and final position of the object then displacement of the object is given by the formula
$\Delta x=x_f-x_i$
where,
$x_f$ is the final position
$x_i$ is the initial position
$\Delta x$ is a change in the position of the object
Now this formula gives the displacement of the object moving in a straight line.
Resultant displacement formula
The resultant displacement formula is used when the distance from the point of reference is used to specify the initial and final position of the object. Despite the fact that distance and displacement are not the same things, displacement problems will tell you how many “foot” or “meters” an object has travelled. Problems would also mention along which direction (North, east, south, west) our object is travelling.
The resultant displacement formula is given by relation
$d=\sqrt{x^2+y^2}$
where, $d$ is displacement.
$x$ is the object’s initial direction of motion and
$y$ is the second direction in which the object moves.
If your object can only move in one direction, $y = 0$.$.
This is the formula for resultant displacement. This formula also gives an equation that shows how to find displacement without using time in physics.
how to calculate displacement
Let us now look at an example problem to find displacement using this formula where the position of the object is given.
Question 1. A car starts to move from point A to point B to point C and then back to point B and then to point C along the line as shown below in the figure.

- find the distance covered by the moving car
- and find the magnitude and direction of the displacement of the car.
Solution.
- distance traveled by car = AB + BC + CB + BC = 11Km+4Km+4Km+4Km = 23Km
- The magnitude of the displacement is equal to the distance between the final point C and the initial point A = AC = 7Km
Since it is an example of motion along a straight line the direction of displacement is along with AB with the vector pointing in the direction from A to B
This was our case for motion along a straight line. we will now look at an example problem where the motion of the object is a case of motion in two different directions.
How to find the magnitude of displacement
Now the questions discussed below will teach you how to find the magnitude of displacement.
Question 2 The path distance from the playground to a school is 9 m west and then 4 m south. A builder wants to build a short-distance path for it. Find the displacement length of the shortest path.
Solution. It is given in the question that
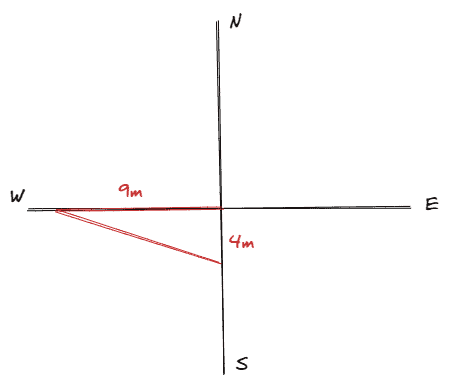
Distance to the west $x = 9 m$
Distance to the south $y = 4 m$
Displacement is given by
$d=\sqrt{x^2+y^2}$
$d=\sqrt{9^2+4^2} = 9.85m$
So, the builder can build a path length of 9.85 m from the playground to the school.
Question 3. An object moves through a distance of 3 miles due east and then 4 miles due north.
- How much is the net distance travelled?
- What is the magnitude of the net displacement?
Solution. The situation described in the question is shown below in the figure. This problem uses the resultant displacement formula for finding the displacement of the object.
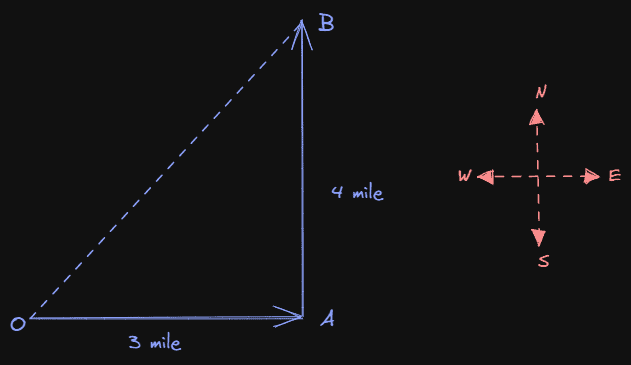
The object starts from O. It moves through a distance of 3 miles due east to reach A and then through a distance of 4 miles due north to reach B.
- The total distance moved is 3 miles +4 miles = 7 miles
- Here OB is the magnitude of net displacement. So from Pythagoras theorem, in a right-angled triangle OAB
$OB^2=OA^2+AB^2$
$=(3\; mile)^2+(4\; mile)^2$
$=25\; mile^2$
or,
$OB=5\; mile$
Question 4. A farmer moves along the boundary of a square field of side 10 m in 40 s. What will be the magnitude of displacement of the farmer at the end of 2 minutes 20 sec?
Solution. The solution to this problem also uses the resultant displacement formula for calculating displacement.
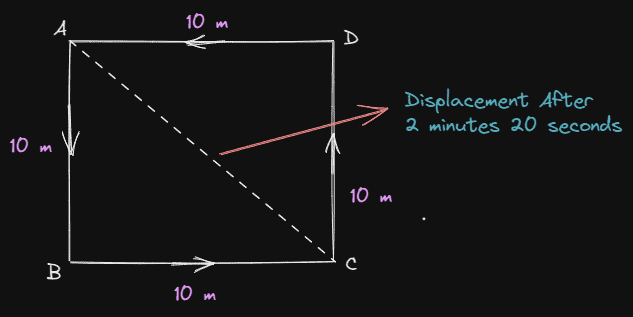
The perimeter of square field ABCD $=4\times 10\; m$
Time for moving around the 10 m square field once = 40 s
Time for journey of the farmer = 2 min and 20 s $= (2\times 60 \;s) +20\; s= 140 \; s$
Number of times farmer moves around the square field $= \frac{140}{40}=3.5 \; times$
For traveling three times around the square field, the displacement $=0$
For traveling half times the square field, the distance covered $=40\;m \times \frac{1}{2}=20\;m$
It can be seen from the figure that if the farmer starts from point A, then he will cover 10 m along with AB and 10 m along with BC.
Therefore, the displacement of the farmer from point A to point C can be calculated using the Pythagoras theorem for a right-angled triangle. So,
$AC=\sqrt{(AB)^2+(BC)^2}=\sqrt{(10)^2+(10)^2}=\sqrt{200}=14.14\; m$