Average velocity is one of the basic concepts students are taught while studying kinematics. Average velocity describes the rate at which an object changes its position over time. It is a vector quantity, which means that it has both a magnitude and a direction.
In this article, we will explore the concept, its equations, and how to calculate it using examples.
Average Velocity Formula
The physical quantity that is numerically equal (i.e. equal in magnitude) to the ratio of the displacement to the time interval is the average velocity of motion over a given period of time.
Mathematically it is given by the formula,
$$v_{avg}=\frac{\Delta x}{\Delta t}=\frac{x_2-x_1}{t_2-t_1}$$
In this equation:
- $v_{avg}$ represents the average velocity $(m/s)$
- $\Delta x$represents the displacement $(m)$
- $\Delta t$ represents the time interval $(s)$
Units of measurement
The units of average velocity are derived from the units of displacement and time. In the International System of Units (SI), the unit of displacement is the meter (m), and the unit of time is the second (s). Therefore, the unit of average velocity is meters per second (m/s).
Additionally, some nonsystem units are also in use, such as:
- Centimeters per second (cm/s): 1 cm/s = $10^(-2)$ m/s
- Kilometers per hour (km/h): 1 km/h = (1000 m)/(3600 s) = 5/18 m/s ≈ 0.278 m/s
- Knot: 1 knot = 1 nautical mile per hour = 1852 m/3600 s ≈ 0.514 m/s
Apart from the units mentioned above, it can also be expressed in other units depending on the specific context or application. Some of these units include:
- Miles per hour (mph): 1 mph = 1 mile per hour ≈ 1.609 km/h ≈ 0.447 m/s
- Feet per second (ft/s): 1 ft/s ≈ 0.305 m/s
It is essential to use appropriate units and convert between them as needed when solving problems.
Solved Example
Suppose an object moves from an initial position $x_1 = 5 ,\text{m}$ to a final position $x_2 = 15 ,\text{m}$ along a straight line over a time interval of $4 ,\text{seconds}$. Let’s calculate the average velocity of the object during this time interval.
Recall the equation for average velocity:
$v_{avg}=\frac{\Delta x}{\Delta t}$
Here,
- $\Delta x$ is the displacement, given by $x_2 – x_1$,
- $\Delta t$ is the time interval.
We can now calculate the displacement:
$\Delta x=x_2−x_1=15m−5m=10m$
The time interval is given as $\Delta t = 4 ,\text{s}$.
Now, we can calculate it using the equation:
$v_{avg}=\frac{\Delta x}{\Delta t}=\frac{10 m}{4s}=2.5sm$
So, the average velocity of the object during the given time interval is $2.5 \text{ m/s}$.
Difference Between Average Speed and Average Velocity
It is crucial to differentiate between average speed and average velocity. While average speed is a scalar quantity representing the total distance traveled divided by the time taken, average velocity is a vector quantity representing the net displacement divided by the time taken. The main differences between speed and velocity are:
- Speed is a scalar quantity, while velocity is a vector quantity.
- Speed has only magnitude, whereas velocity has both magnitude and direction.
- Average speed can never be negative, while average velocity can have negative values based on the direction of the displacement.
| Average Speed | Average Velocity | |
|---|---|---|
| Definition | Total distance traveled divided by total time taken | Displacement divided by time interval |
| Scalar or Vector | Scalar (magnitude only) | Vector (magnitude and direction) |
| Affected by Direction | No | Yes |
When is the average velocity zero?
The average velocity of an object is zero when the displacement over a given time interval is zero. This can occur when an object returns to its initial position or when it remains stationary for the entire time interval.
Let’s consider an example. A person starts walking from point A in a straight line, covers a distance of 5 meters, and reaches point B. Then, the person turns around and walks back to point A, covering the same distance of 5 meters. The total displacement is zero because the person has returned to the initial position.
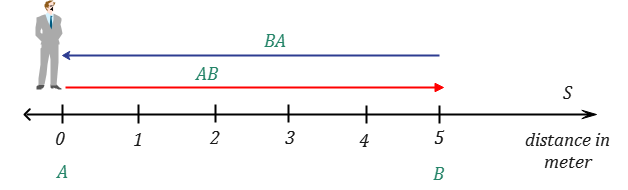
The equation for average velocity is:
$v_{avg}=\frac{\Delta x}{\Delta t}$
Here, $\Delta x$ is the displacement and $\Delta t$ is the time interval. Since the displacement is zero, the average velocity becomes zero, regardless of the time interval:
$v_{avg}=\frac{0}{\Delta t}=0$
In this example, the average velocity is zero because the net displacement over the entire journey is zero.
Common mistakes and misconceptions
- Confusing average velocity with average speed: Average speed is a scalar quantity that only considers the magnitude of distance traveled over time, while average velocity is a vector quantity that considers both the magnitude and direction of the displacement over time.
- Assuming that average velocity remains constant throughout the motion: In variable motion, the average velocity depends on the choice of the time interval. For uniform motion, the average velocity remains constant, but in non-uniform motion, it can change depending on the time interval selected.
- Believing that average velocity is always equal to the instantaneous velocity: The average velocity represents the overall rate of displacement during a time interval, while the instantaneous velocity is the rate of displacement at a specific point in time. In uniform motion, average velocity and instantaneous velocity may be equal; however, in non-uniform motion, they can differ.
Summary
In summary, average velocity is a vector quantity that provides information about the rate of displacement of an object during a given time interval. It is crucial to consider both the magnitude and direction of the displacement and be familiar with the various units and types of velocity to analyze and solve problems related to motion accurately.