Radial Force Equation
When an object moves along a circular path, it experiences a force directed towards the center of the circle. This force is known as the radial or centripetal force. The term ‘centripetal’ comes from the Latin words ‘centrum,’ meaning center, and ‘petere,’ meaning to seek. In this article, we will look into the formula of radial force, its physical significance, and its various applications.
Definitions
Centripetal Acceleration
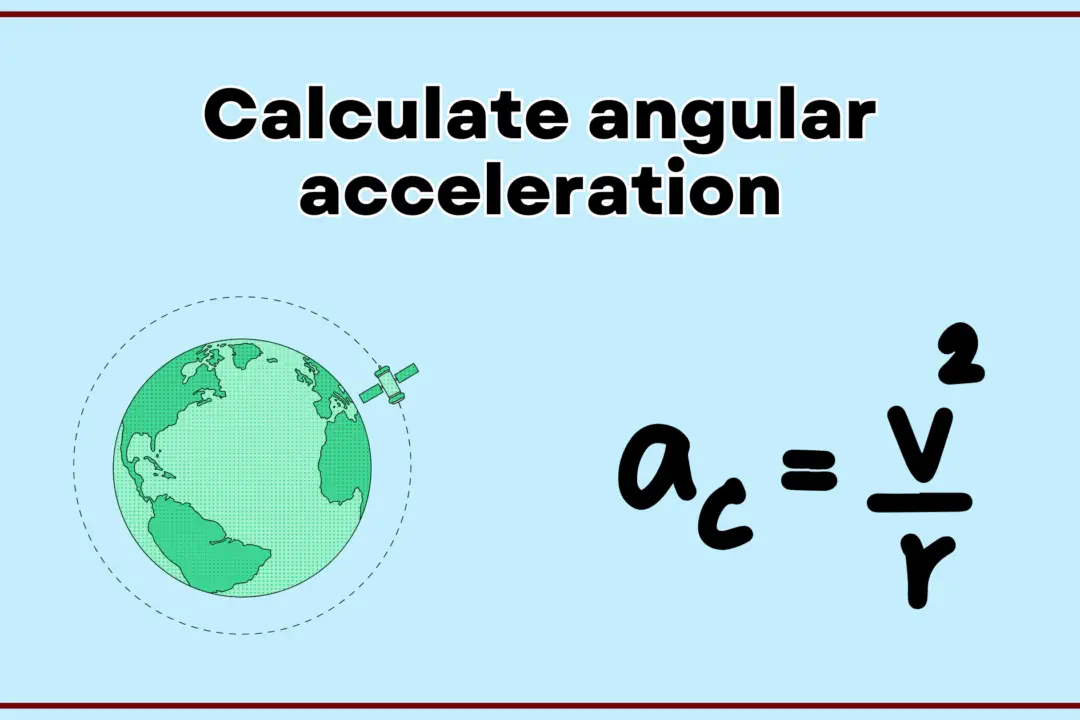
Centripetal acceleration (\( a_c \)) is the rate of change of tangential velocity and is directed towards the center of the circle. The formula for centripetal acceleration is:
\[
a_c = \frac{{v^2}}{r}
\]
where \( v \) is the magnitude of the velocity and \( r \) is the radius of the circular path.
Radial or Centripetal Force
Centripetal force (\( F_c \)) is the force that keeps an object moving in a circular path. The magnitude of this force is determined by the equation:
\[
F_c = m \times a_c
\]
Substituting the expression for \( a_c \) into the above equation, we get:
\[
F_c = m \times \frac{{v^2}}{r}
\]
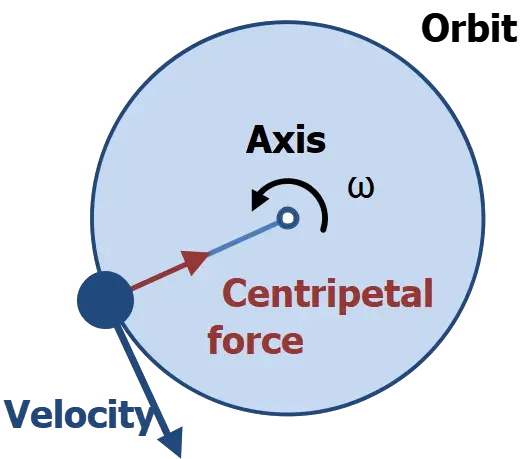
Derivation of Radial Force Equation
The centripetal force can be derived using Newton’s second law, which states that the sum of all forces acting on an object is equal to the mass of the object multiplied by its acceleration (\( F = ma \)).
For an object moving in a circle of radius \( r \) at a constant speed \( v \), the centripetal acceleration can be expressed as \( a_c = \frac{{v^2}}{r} \).
1. Identify Forces:
For an object in a circular motion, the net force is the centripetal force (\( F_c \)) acting towards the center of the circle.
2. Apply Newton’s Second Law:
We apply Newton’s second law in the radial direction (toward the center of the circle):
\[
F_c = m \times a_c
\]
3. Substitute Centripetal Acceleration:
Replace \( a_c \) with its expression in terms of velocity \( v \) and radius \( r \):
\[
F_c = m \times \frac{{v^2}}{r}
\]
4. Simplification:
The formula doesn’t require any further simplification as it directly gives us the centripetal force in terms of known quantities \( m \), \( v \), and \( r \).
By combining Newton’s second law with the concept of centripetal acceleration, we arrive at the equation \( F_c = m \times \frac{{v^2}}{r} \). This equation quantitatively describes the radial force required to keep an object in uniform circular motion.
Applications
- In planetary motion, the gravitational force acts as the centripetal force that keeps planets in orbit.
- In vehicles taking a turn, the frictional force between the tires and the road serves as the centripetal force.
- Centrifuges use the concept of centripetal force to separate substances of different densities.
Questions and Answers
Can centripetal force be negative?
No, centripetal force is always directed towards the center of the circular path, and its magnitude is always positive.
How does mass affect centripetal force?
The centripetal force is directly proportional to the mass. A greater mass would require a greater centripetal force to keep it in circular motion.
What happens if centripetal force is removed?
If the centripetal force is removed, the object would move in a straight line along the path of its instantaneous velocity at the point where the force is removed, according to Newton’s first law of motion.
Why is centripetal acceleration squared in the formula?
The square of the velocity in the formula for centripetal acceleration (\( a_c = \frac{{v^2}}{r} \)) arises from the vector nature of velocity and acceleration. The speed might be constant, but the direction of the velocity vector is continually changing, hence the squared term in acceleration.
Further Reading
By understanding the radial force equation, one gains a critical insight into the mechanics of circular motion and the forces required to sustain or modify such motion. This equation has vast implications, from explaining planetary orbits to designing efficient rotating machinery.