Introduction
Uniform motion plays a significant role in understanding the movement of objects in our everyday lives. In this article, we will learn about the concept of uniform motion in physics. We will also learn about its graphical representation along with the initial instant of time. In the end, I will discuss some of the frequently asked questions about this concept.
We will also provide a quiz at the end of the article where you can check your understanding of uniform motion in physics.
Understanding Uniform Motion:
Uniform motion definition:
Uniform motion is defined as the motion of a particle whose coordinate (position) is a linear function of time.
The equation for this type of motion is $x = vt + b$, where $v$ and $b$ are constants. Any motion that does not fit this definition is considered variable motion.
Equation of Motion:
The equation $x = vt + b$, represents uniform motion, where $x$ is the coordinate of the particle, $v$ is the constant velocity, $t$ is the time, and $b$ is the initial position.
Graphical Representation of Uniform Motion:
Importance of graphs
Illustrations, such as graphs, are crucial for understanding complex concepts in physics, including uniform and variable motion. They provide a visual representation of the motion, allowing for easier interpretation and analysis of the motion’s characteristics.
Visualizing Motion – Plotting a Graph:
The motion equation can be visually represented by plotting a graph. This is done by constructing a coordinate system with time (t) on the x-axis and the particle’s coordinate (x) on the y-axis.
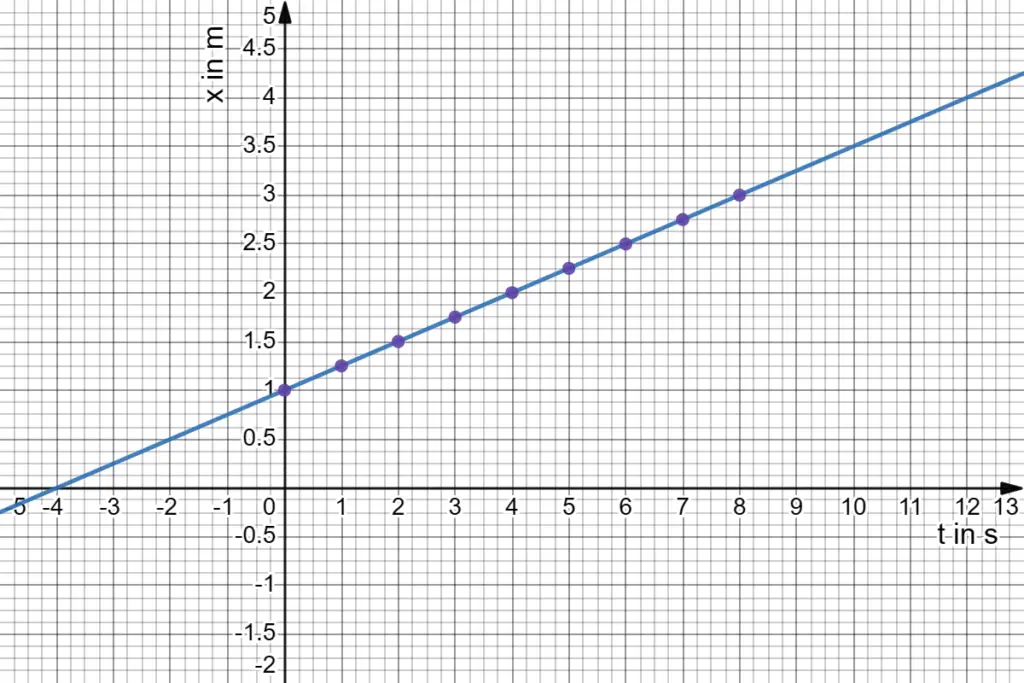
To better understand this, consider the data from our article on Rectilinear Motion. The table given below shows the measurements of the car’s position in relation to the markers at regular intervals of time.
| Instant of time $t$ in seconds | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Coordinate $x$ in meter | 1 | 1.25 | 1.50 | 1.75 | 2.00 | 2.25 | 2.50 | 2.75 |
By plotting the values of the variables from the table on both axes, we proceed to create perpendicular lines from the axes at these points. The intersection of these perpendicular lines forms a series of points.
Drawing a smooth line connecting these points results in a motion graph. As the coordinate in uniform motion is a linear function of time, the resulting graph appears as a straight line as shown below in the figure.
The Initial Instant of Time:
The initial instant of time is the point at which an experiment or observation begins. It is not necessarily the beginning of the motion but rather the starting point of the study.
About Initial Coordinate:
The initial coordinate, denoted by $x_0$, is the distance from the moving particle to the origin of coordinates at the initial instant of time. This can be determined by setting $t = 0$ in the equation of motion, which gives $x_0 = b$.
Example of uniform motion
List of few other examples of uniform motion
- The revolution or orbital motion of the Earth around the Sun.
- Earth’s rotation about its axis
- A man-made satellite orbiting the Earth.
- Walking at a steady speed.
- The hour hand of the clock
- A car traveling at a constant speed along a straight, flat route.
- A sewing machine’s vibrating spring.
Challenges and Limitations:
Although the uniform motion is a fundamental concept in physics, real-world applications often involve variable motion due to factors such as friction, air resistance, and changing forces. Therefore, uniform motion serves as a basis for understanding more complex motion scenarios.
Frequently asked questions
1. What is the difference between uniform and non-uniform motion with examples?
Uniform motion occurs when an object moves at a constant speed in a straight line. In this case, the object covers equal distances in equal intervals of time. For example, a car traveling at a constant speed of 60 km/h on a straight highway exhibits uniform motion.
Non-uniform motion, on the other hand, occurs when an object’s speed, direction, or both change over time. The object does not cover equal distances in equal intervals of time. For example, a roller coaster with varying speeds and changing directions demonstrates non-uniform motion.
2. What is the purpose of uniform motion in physics, and how is it used in everyday life?
Uniform motion is a fundamental concept in physics that helps us understand the motion of objects in the real world. It forms the basis for understanding more complex motion patterns and phenomena. In everyday life, uniform motion can be seen in various situations, such as a person jogging at a constant pace around a track or a conveyor belt moving at a steady speed in a factory.
3. How can one maintain uniform motion?
To maintain uniform motion, an object must maintain a constant speed and move in a straight line. This can be achieved by ensuring that no external forces act upon the object, or that the net force acting on the object is zero. In practice, this can be difficult due to factors such as friction, air resistance, and changes in terrain or environment.
4. What does the path of an object look like when it’s in uniform motion?
When an object is in uniform motion, its path is a straight line. This is because the object moves at a constant speed without changing direction. The graphical representation of uniform motion, with time on the horizontal axis and position on the vertical axis, would also appear as a straight line.
5. Does a body subjected to uniform motion always move in a straight line?
Yes, a body subjected to uniform motion always moves in a straight line. This is because uniform motion is characterized by constant speed and unchanging direction. Any deviation from a straight-line path would indicate a change in direction, which would mean the motion is no longer uniform.

