Learn how to find average acceleration in physics in this article. It is a crucial topic in kinematics. Let us begin with a basic overview of the idea of acceleration in physics.
Key Takeaways
- Remember that acceleration is a vector quantity with both magnitude and direction.
- Use the formula
$a_{\text{avg}} = \frac{(v_f – v_i)}{(t_f – t_i)}$
to find the average acceleration. - Remember the units for acceleration (m/s²) and ensure your calculations are consistent with these units.
- Positive acceleration indicates an increase in velocity, while negative acceleration indicates a drop in velocity.
Finding average acceleration
Introduction to Acceleration
Acceleration is a measure of how quickly an object’s velocity changes. It indicates the rate at which an object accelerates or decelerates. Acceleration is a vector quantity in physics, which means it has both magnitude (size) and direction. Acceleration is measured in meters per second squared $(m/s^2)$.
Average Acceleration Formula
The average acceleration is calculated by dividing the change in velocity by the change in time. It is represented mathematically as:
$a_{avg} = \frac{v_f – v_i}{t_f – t_i}$
where:
$a_avg$ is the average acceleration
$v_f$ is the final velocity
$v_i$ is the initial velocity
$t_f$ is the final time
$t_i$ is the initial time
It is important to note that if the velocity of an object increases over time, the average acceleration will be positive. The average acceleration will be negative if the velocity decreases over time.
Example Problem
To better understand the concept of average acceleration, consider the following example:
Consider a car that starts from rest and accelerates to 30 m/s in 10 seconds. Find the average acceleration of the car.
Given:
Initial velocity (v_i): 0 m/s (since the car starts from rest)
Final velocity (v_f): 30 m/s
Initial time (t_i): 0 s (assuming time starts when the car begins to move)
Final time (t_f): 10 s
Using the formula:
$a_{\text{avg}} = \frac{(v_f – v_i)}{(t_f – t_i)}$
$a_{\text{avg}} = \frac{(30 \text{ m/s} – 0 \text{ m/s})}{(10 \text{ s} – 0 \text{ s})}$
$a_{\text{avg}} = \frac{(30 \text{ m/s})}{10 \text{ s}}$
$a_{\text{avg}} = 3 \text{ m/s}^2$
The average acceleration of the car is 3 m/s².
Different ways to find average acceleration
There are different ways to find average acceleration, depending on the available information and the specific situation. Here, we will discuss three common methods to find average acceleration:
- Using the formula for average acceleration
- From a velocity-time graph
- Using equations of motion
Using the formula for average acceleration
As explained previously, we can use the formula $a_{\text{avg}} = \frac{(v_f – v_i)}{(t_f – t_i)}
$ to calculate the average acceleration when we have information about the initial and final velocities and the initial and final times.
Example: A car accelerates from 0 m/s to 20 m/s in 5 seconds. Find its average acceleration.
Using the formula:
$a_{\text{avg}} = \frac{(20 \text{ m/s} – 0 \text{ m/s})}{(5 \text{ s} – 0 \text{ s})}$
gives
$a_{\text{avg}} = \frac{20 \text{ m/s}}{5 \text{ s}}$
$a_{\text{avg}} = 4 \text{ m/s}^2$
From a velocity-time graph
If we have a graph that plots an object’s velocity against time, we can find the average acceleration by calculating the slope of the line connecting the initial and final points.
Example: Consider a velocity-time graph where a car starts at 0 m/s and reaches 20 m/s in 4 seconds.
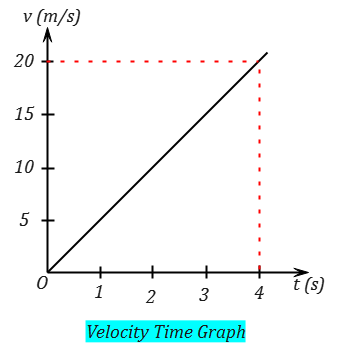
In this case, the slope (rise/run) equals the change in velocity $20 \text{ m/s} – 0 \text{ m/s}$ divided by the change in time $4 \text{ s} – 0 \text{ s}$.
The average acceleration is, therefore,
$a_{\text{avg}} = \frac{20 \text{ m/s}}{4 \text{ s}}$
$a_{\text{avg}} = 5 \text{ m/s}^2$
Using equations of motion
When we have information about an object’s displacement and time but not its final velocity, we can use the equations of motion to find the average acceleration. For uniformly accelerated motion, one such equation is:
$v_f^2 = v_i^2 + 2a(x_f – x_i)$
where:
$v_f$ is the final velocity
$v_i$ is the initial velocity
$a$ is the average acceleration
$x_f$ is the final position
$x_i$ is the initial position
Example: A car starts from rest and covers a distance of 50 meters in 10 seconds. Find its average acceleration.
First, use the equation of motion to find the final velocity:
$v_f^2 = 0 \text{ m/s}^2 + 2a(50 \text{ m} – 0 \text{ m})$
We need to find $a$
Rearrange the equation to solve for $a$:
$a = \frac{v_f^2}{2 \cdot 50 \text{ m}}$
Since we don’t have the final velocity, we can use another equation of motion to find it:
$x_f = x_i + v_i \cdot t + 0.5 \cdot a \cdot t^2$
Rearrange to solve for $v_f$:
$v_f = \frac{x_f – x_i – 0.5 \cdot a \cdot t^2}{t}$
Here,
$v_f = \frac{50 \text{ m} – 0 \text{ m} – 0.5 \cdot a \cdot (10 \text{ s})^2}{10 \text{ s}}$
Square the above expression and substitute it back into the first equation to solve for $a$. After simplifying, we get
$a = 1 \text{ m/s}^2$
These are three different ways to find average acceleration, depending on the available information and the specific situation.
The Importance of Sign Convention
- Average acceleration problems need the correct use of signs.
- Positive and negative signs show directions (left-right, up-down).
- Using signs right helps get correct answers.
- Look at the problem’s context and coordinate system.
- Choose the proper sign convention for the situation.
Quiz