Pivot Point Definition
A pivot point in physics is a fixed point around which an object rotates or balances. It serves as the axis of rotation for a rigid body and is the reference point for calculating torque (rotational force). Pivot points are fundamental to understanding rotational motion, levers, and equilibrium.
Basic Concept and Definition
A pivot point (also called a fulcrum) is the point that remains stationary while other parts of an object move around it. When forces act on an object, they can cause rotation around the pivot point.
Key characteristics of pivot points:
- They experience zero linear displacement during rotation
- All torque calculations are made with respect to the pivot
- They serve as the origin for measuring moment arms

Pivot Points and Torque
Torque is the rotational equivalent of force and depends critically on the location of the pivot point. The mathematical expression for torque is:
$$\tau = r \times F \sin\theta$$
Where:
- $\tau$ (tau) is the torque
- $r$ is the distance from the pivot point to where the force is applied
- $F$ is the applied force
- $\theta$ is the angle between the position vector and force vector
Alternatively, torque can be expressed as:
$$\tau = r_{\perp} F$$
Where $r_{\perp}$ is the perpendicular distance from the pivot to the line of action of the force.
Pivot Points in Equilibrium Problems
For an object to be in rotational equilibrium, the net torque about any pivot point must be zero:
$$\sum \tau = 0$$
Choosing the right pivot point can greatly simplify equilibrium problems by eliminating unknown forces from your calculations. For example, selecting a pivot at a point where an unknown force acts means that force contributes zero torque (as $r = 0$).
Static vs. Dynamic Pivot Points
- Static pivot points remain fixed relative to an inertial reference frame (like a door hinge)
- Dynamic pivot points can move linearly while serving as rotation axes (like a rolling wheel’s instantaneous point of contact with the ground)
Applications in Everyday Physics
Pivot points are essential in understanding:
- Levers and simple machines
- Seesaw and balance problems
- Door operation
- Human joint movements
- Angular momentum conservation
How to find the pivot point physics
When solving physics problems:
- Identify the object’s axis of rotation or the point about which torque is calculated
- Look for fixed supports, hinges, or points of contact that constrain motion
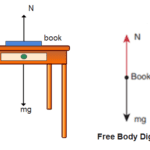
- In free-body diagrams, mark the pivot with a dot or circle
- For objects in equilibrium, any point can be chosen as a pivot (though some choices simplify calculations)
- For rigid objects undergoing rotation, the pivot is typically where the rotational axis passes through the object
- For systems with multiple objects, different pivot points may be needed for each component