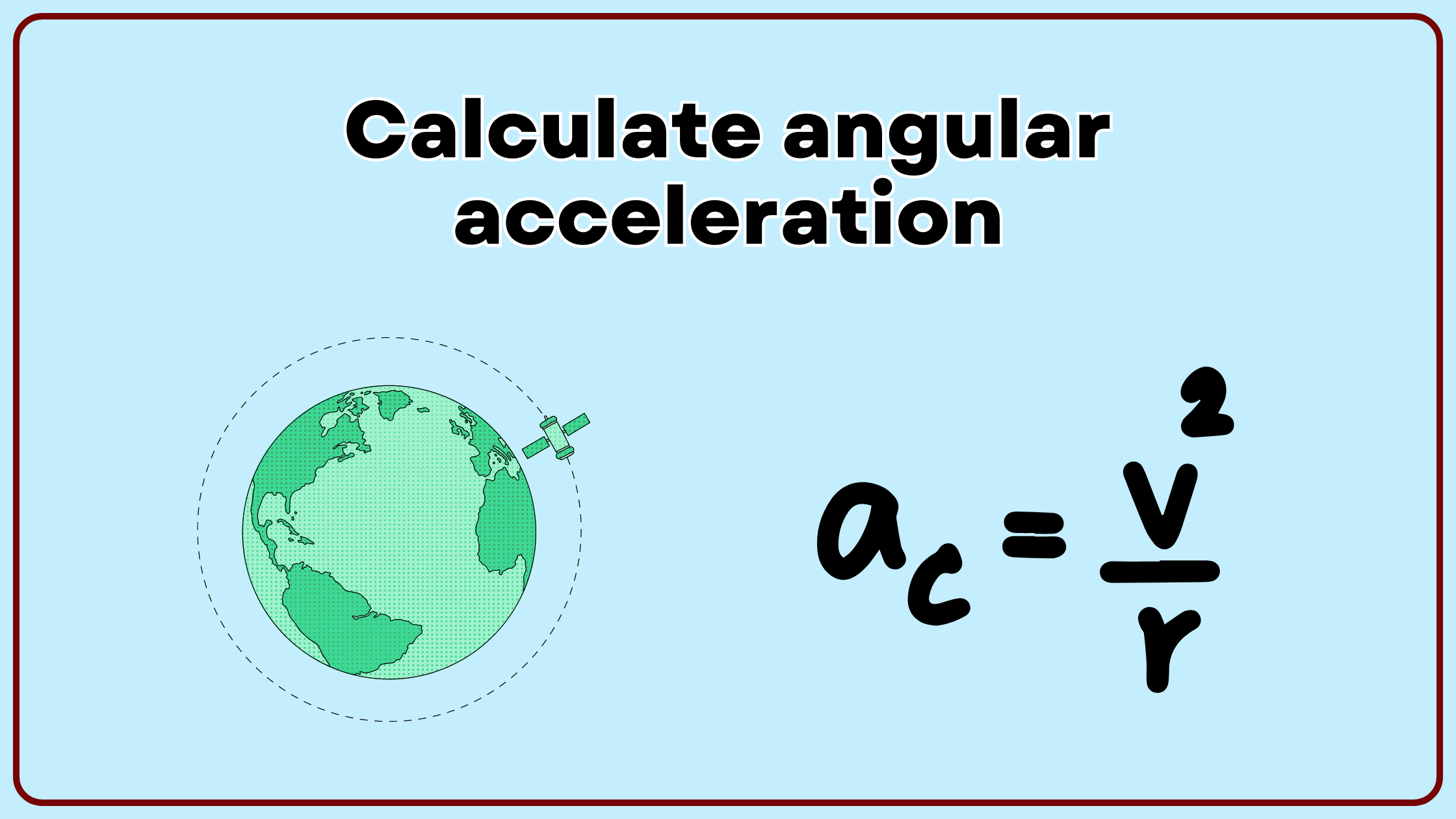
In this article learn how to calculate angular acceleration. We study angular acceleration when we study rotational motion. Angular acceleration is a concept that students must understand in order to understand the dynamics of objects moving in circular paths, from spinning wheels to celestial bodies orbiting around each other.
See also: formula for acceleration
Angular Acceleration: A Quick Overview
Before getting into several ways to calculate angular acceleration, let’s take a moment to understand what is angular acceleration in physics. Angular acceleration \(\alpha\) is the rate at which an object’s angular velocity changes with time. In other words, it measures how quickly the rotational speed of an object is increasing or decreasing.
Angular acceleration is a vector quantity, which means it has both magnitude and direction. Its units are radians per second squared (rad/s²) in the SI system.
Key Takeaways on calculating angular acceleration
- The definition formula for angular acceleration is α = Δω / Δt.
- You can calculate the angular acceleration using different formulas depending on the available information.
- One way to calculate the angular acceleration is by using angular velocity and time.
- Another method to find the angular acceleration is using torque and moment of inertia.
- You can also calculate the angular acceleration using tangential acceleration and radius.
- The formula for angular acceleration is α = (ω – ω₀) / Δt = Δω / Δt.
- The moment of inertia formula can also be used to calculate the angular acceleration: $\alpha = \frac{\tau}{I}$.
- The formula for tangential acceleration can be used to find the angular acceleration: $\alpha =\frac{a_t}{r}$.
Calculating Angular Acceleration
There are several ways to calculate angular acceleration, depending on the available information. We will discuss three common methods to calculate angular acceleration.
Using angular velocity and time:
If you know the initial angular velocity (ω₀), the final angular velocity (ω), and the time interval (Δt) during which the acceleration occurs, you can calculate angular acceleration using the following formula:
α = (ω – ω₀) / Δt
How to find angular acceleration with angular velocity
Problem:
A spinning wheel starts from rest and reaches an angular velocity of 40 rad/s in 8 seconds. Calculate the angular acceleration of the wheel.
Solution:
Step 1: Identify the given information
Initial angular velocity (ω₀) = 0 rad/s (starts from rest)
Final angular velocity (ω) = 40 rad/s
Time interval (Δt) = 8 s
Step 2: Apply the formula for angular acceleration
α = (ω – ω₀) / Δt
Step 3: Plug in the given values into the formula
α = (40 rad/s – 0 rad/s) / 8 s
Step 4: Calculate the angular acceleration
α = (40 rad/s) / 8 s α = 5 rad/s²
The angular acceleration of the spinning wheel is 5 rad/s².
Using torque and moment of inertia:
If you know the net torque (τ) acting on an object and its moment of inertia (I), you can calculate angular acceleration using Newton’s second law for the rotational motion:
$\alpha = \frac{\tau}{I}$
The moment of inertia depends on the mass distribution of the object and the axis of rotation. For common shapes, the moment of inertia can be looked up in reference tables or calculated using specific formulas.
How to calculate angular acceleration from moment of inertia
Through the problem given below let us understand how do you find angular acceleration from moment.
Problem:
A solid cylinder with a mass of 10 kg and a radius of 0.5 m is subjected to a net torque of 15 Nm. Calculate the angular acceleration of the cylinder.
Solution:
Step 1: Identify the given information
Mass (m) = 10 kg
Radius (r) = 0.5 m
Net torque (τ) = 15 Nm
Step 2: Calculate the moment of inertia (I) for a solid cylinder
The moment of inertia for a solid cylinder rotating about its central axis is given by the formula:
$I = (1/2) m r^2$
Step 3: Plug the given values into the moment of inertia formula
$I = (1/2) \times 10 kg \times (0.5 m)^2$
$I = 5 kg \times 0.25 m^2$
$I = 1.25 kgm^2$
Step 4: Apply the formula for angular acceleration using torque and moment of inertia
$\alpha = \frac{\tau}{I}$
Step 5: Plug in the given values into the formula
$\alpha = \frac{15 Nm}{1.25 kgm^2}$
Step 6: Calculate the angular acceleration
α = 12 rad/s²
The angular acceleration of the solid cylinder is 12 rad/s².
This is how you calculate angular acceleration from torque.
Using centripetal and tangential acceleration
In some cases, you may have information about an object’s tangential acceleration $(a_t)$ at a specific point on its path.
Tangential acceleration describes the change in linear velocity for an object moving in a circular path, while angular acceleration deals with the change in angular velocity.
Both are vector quantities; however, tangential acceleration acts along the path’s tangent, whereas angular acceleration is directed along the rotation axis.
If you know the object’s radius (r) of the circular path and tangential acceleration, you can calculate angular acceleration using the following angular acceleration formula with radius:
$\alpha = a_t / r$
Both tangential and angular acceleration are related through the equation $a_t = \alpha \times r$, connecting linear (tangential) and rotational (angular) aspects of circular motion. This formula gives angular acceleration formula with linear acceleration.
Calculating Angular Acceleration using Tangential Acceleration
This problem also shows how to find angular acceleration without time. Here you only have information about its tangential acceleration and radius of the circular path.
Problem:
An object is moving in a circular path with a radius of 2 m. At a certain point on the path, its centripetal acceleration is 20 m/s², and its tangential acceleration is 10 m/s². Calculate the angular acceleration at that point.
Solution:
Step 1: Identify the given information
Centripetal acceleration (a_c) = 20 m/s²
Tangential acceleration (a_t) = 10 m/s²
Radius (r) = 2 m
Step 2: Apply the formula for angular acceleration using tangential acceleration and radius
$\alpha = a_t / r$
Step 3: Plug in the given values into the formula
α = 10 m/s² / 2 m
Step 4: Calculate the angular acceleration
α = 5 rad/s²
The angular acceleration of the object at that specific point on the circular path is 5 rad/s².
It is important to note here that if you have information about radius and tangential acceleration then you can convert linear acceleration to angular acceleration.