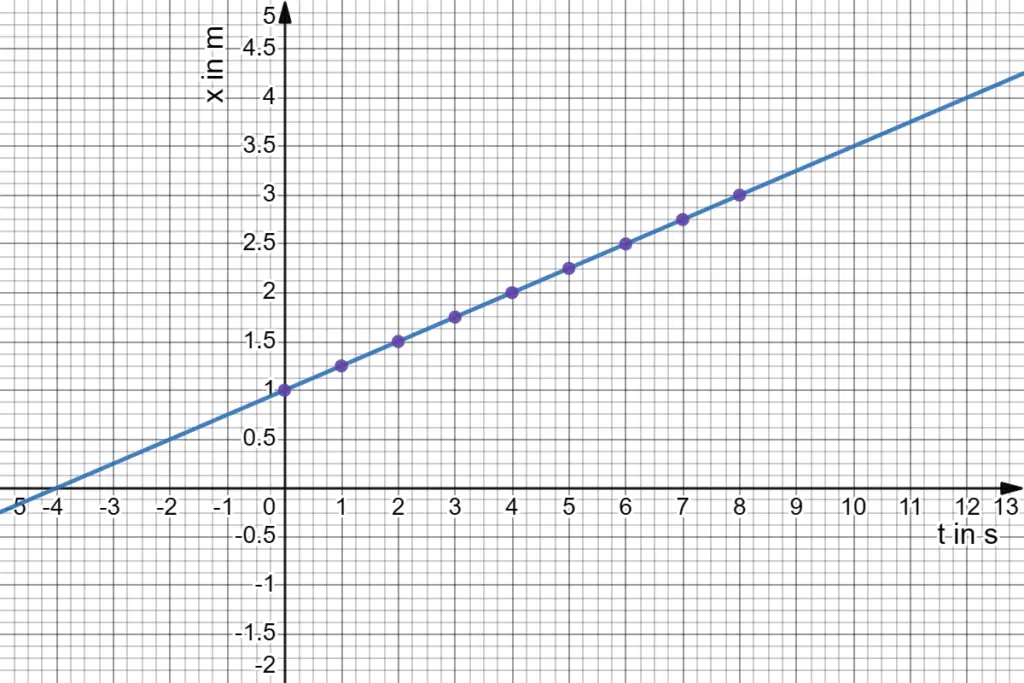
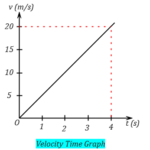
Welcome to constant acceleration problems. In this article, we will first have a look at kinematics equations for objects moving under constant acceleration.

The simplest form of accelerated motion is motion in a straight line with constant acceleration. Because acceleration is always the same, the velocity changes at the same rate as time moves on.
Most homework problems involving motion under constant acceleration may be solved using three fundamental formulas.
These equations of motion of a moving particle with constant acceleration $a$ are
- $v=v_0+at$
- $x=x_0+v_0t+\frac{1}{2}at^2$ or sometimes written as, $d=v_0t+\frac{1}{2}at^2$
- $v^2=v_0^2+2a(x-x_0)$ or sometimes written as, $v^2=v_0^2+2ad$
Here,
$v_0$ is the initial [[velocity]] of the particle and
$v$ is the final velocity of the particle.
$x_0$ is the initial position of the particle
$x$ is the distance traveled by the particle in time $t$.
$a$ is the acceleration of the moving particle
Most of the time initial velocity $v_0$ and initial position $x_0$ is zero. $(x-x_0)$ is displacement from the starting position and is sometimes denoted as letter $d$ or $s$.
Read about How to solve kinematics problems
Constant Acceleration problems with answers
Question 1. A motorbike accelerates uniformly from 12.5 m/s to 35.5 m/s in 5 seconds. Determine the acceleration of the bike and the distance traveled by it.
Solution 1. It is given in the question that
initial velocity $v_0=12.5 m/s$, final velocity $v=35.5m/s$ and $t=5s$
We have to find distance traveled $d=?$ and acceleration $a=?$
acceleration
$a=\frac{\text{change in velocity}}{\text{time taken}}=\frac{\Delta v}{t}=\frac{35.5m/s – 12.5 m/s}{5s}$
or,
$a=4.6ms^{-2}$
distance traveled can be calculated using kinematic equation
$d=v_0t+\frac{1}{2}at^2$
since we have knowledge of quantities $v_0$, $a$ and $t$.
putting in the respective values in above equation we get
$d=(12.5 m/s \times 5)+\frac{1}{2}(4.6ms^{-2}\times (5)^2)$
or,
$d=62.5m+57.5m=120 m$
Note:- $d$ can also be calculated using the equation $v^2=v_0^2+2ad$
Question 2. A car moving along a straight highway with a speed of $72\, Km/h$ is bought to stop within a distance of 100 m. What is the retardation of the car and how long does it take for the car to stop?
Solution 2.
Given that
initial velocity $v_0=72\, Km/h=\frac{72\times 5}{18}=20m/s$
final velocity $v=0$
distance traveled $x-x_0=100 m$
acceleration $a=?$
From equations of motion of constant acceleration we know that
$v^2=v_0^2+2a(x-x_0)$
$0^2 – (20)^2 =2a\times 100$
or,
$a=-2m/s^2$
$\text{Retardation}=-2m/s^2$
Required time,
$t=\frac{v-u}{a}=\frac{0-20}{-2}=10s$
Question 3. A car moving with a velocity of $10m/s$ accelerates uniformly at $1m/s^2$ until it reaches a velocity of $15m/s$. Calculate
(i) the time taken
(ii) the distance traveled during acceleration
(iii) the velocity reached 100m from the place where acceleration begins.
Solution 3.
Given that
initial velocity $v_0=10m/s$
final velocity $v=15m/s$
acceleration $a= 1m/s^2$
We have to find
(i) The time taken by the car.
using first equation of motion
$v=v_0+at$
$15=10+1(t)$
solving it for $t$ we get $t=5s$
(ii) The distance travelled by the car.
Using second equation of motion
$d=v_0t+\frac{1}{2}at^2$
$d=(10\times 5)+\frac{1}{2}\times 1 \times (5)^2$
solving it for $s$ we get $d=62.5 m$
(iii) Using third equation of motion
$v^2-v_0^2=2ad$
$v^2=(15)^2+2\times 1\times 100=225+200=425$
$v=20.6m/s$ is the velocity reached 100m from the place where acceleration begins.
Question 4. An bike’s velocity increases uniformly from $3 m/s$ to $15 m/s$ while covering $60 m$. Find the acceleration and the time taken.
solution 4. We are given that
final velocity $v=15m/s$ and
initial velocity $v_0=3m/s$
displacement $d=60m$
Since we do not have any information about time taken to cover the displacement, we can find acceleration using the equation
$v^2-v_0^2=2ad$
putting in the values we gat
$(15)^2-(3)^2 = 2\times a \times 60$
solving the above equation for acceleration $a$ we get
$a=\frac{225-9}{2\times 60}=\frac{216}{120}=1.8m/s^2$
Thus $a=1.8m/s^2$
Now, $t$ can be calculated using the relation
$v=v_0+at$
putting in the values we gat
$15=3+1.8\times t$
or,
$t=\frac{15-3}{1.8}=6.67s$
Question 5. The reaction time for an automobile driver is 0.7 seconds. If the automobile can decelerate at $5 ms^{-2}$, calculate the total distance traveled in coming to stop from an initial velocity $30Km/hr$ after the signal is observed.
Solution 5.
Since the reaction time of the driver is 0.7 seconds therefore during this time the automobile will continue to move with a uniform velocity of $30Km/hr$.
Since units of all other quantities are given in SI system we would first convert velocity from $Km/hr$ to $m/s$
We know that
1 Km =1000 m and
1 hour = 3600 seconds
$\Rightarrow \; 30Km/hr=\frac{30\times 1000}{3600}ms^{-1}=\frac{25}{3}ms^{-1}$
Distance covered during 0.7 second $= \frac{25}{3}ms^{-1} \times 0.7s=5.83m$
Let us choose that time as a reference time (t=0) when the automobile begins to decelerate.
So at
$t=0$, $x_0=0$, $v_0=\frac{25}{3}ms^{-1}$, $a=-5ms^{-2}$
We have to find $x$ and final velocity $v=0$
Equation of motion we use hare is
$v^2=v_0^2+2a(x-x_0)$
since we have to find $x$ and we have knowledge about quantities $a$ and $v_0$.
Putting in the values in above equation we get
$0^2=\frac{25}{3}+2(-5)(x-0)$
or,
$x=\frac{625}{9}\times\frac{1}{10}m=6.94m$
Total distance travelled $=5.83\, m + 6.94\, m=12.77\,m$
Question 6. A ball is thrown upwards with a velocity of $78.4 ms^{-1}$. Find how high it will rise and how much time it will take to return to its point of projection.
Solution 6.
Let O be the point of projection and is taken as origin.
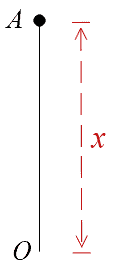
Given:
At $t=0$, velocity $v_0=78.4 ms^{-1}$
Let $t$ be the time taken to reach the maximum height. Then,
$v=0$
since velocity is zero at maximum height. Also
$x_0=0$ at time $t=0$ and acceleration $a=-9.8ms^{-2}$
here $a$ is the acceleration due to gravity which acts in a downwards direction. The negative sign is taken because the upwards direction is taken a $+ive$ direction.
To Find:
how high does the ball rise $x=?$
and total time = time of ascent (t)+time of descent (t) = 2t
since the time of ascent is equal to the time of descent.
Now,
$v^2=v_0^2+2a(x-x_0)$
$0^2-(78.4)^2=2(-9.8)[x-0]$
or,
$x=\frac{78.4\times 78.4}{2\times 9.8}m=313.6m$
Again,
$v=v_0+at$
$0=78.4+(-9.8)t$
rearranging it we get
$t=\frac{78.4}{9.8}s$
or,
$t=8s$
$\text{total time} = \text{time of ascent} (t)+\text{time of descent} (t) = 2t$
$\Rightarrow\, \text{Total time}=8s+8s=16s$