How does centripetal acceleration differ from linear acceleration?

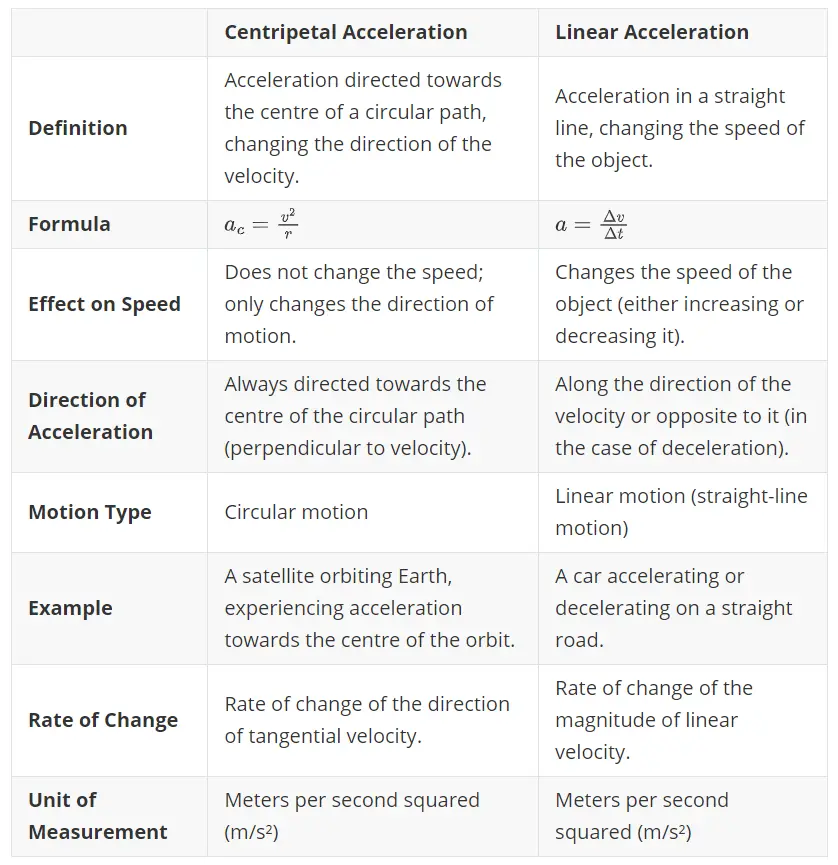
Centripetal acceleration occurs when an object is traveling in a circular path, whereas linear acceleration happens when an object is moving in a straight line.

Linear Acceleration:

This is the rate of change of linear velocity, which refers to the velocity of an object moving in a straight line. When an object speeds up or slows down, its velocity changes, and this change in speed is caused by linear acceleration.

For example, if you drop a satellite from a height, gravity will cause it to accelerate towards the ground in a straight line. The satellite experiences linear acceleration as its speed increases on the way down. When it hits the ground, linear acceleration in the opposite direction (due to impact) would cause it to slow down.

Key Characteristics:

Direction: Linear acceleration is always in the direction of the velocity of the object (along the tangent to the path, in case of a curve).
Formula: $a = \frac{\Delta v}{\Delta t}$ where $a$ is the acceleration, $\Delta v$ is the change in velocity, and $\Delta t$ is the time interval.
Example: When you press the gas pedal in a car, the car speeds up in a straight line. The change in the car’s velocity over time is an example of linear acceleration.

Centripetal Acceleration:

In contrast, centripetal acceleration refers to the rate of change of tangential velocity, which is the velocity of an object moving along a circular path. Even though the object’s speed remains constant, centripetal acceleration continuously alters the direction of the velocity, which keeps the object in a curved path.

Imagine the same satellite, but now it has been successfully launched into a circular orbit. Once in orbit, the only acceleration it experiences is centripetal, which always points toward the center of its circular path (in this case, toward the Earth). This acceleration doesn’t increase or decrease the satellite’s speed—it just keeps it moving in a circle by constantly changing its direction.

Centripetal Acceleration Key Characteristics:

Direction: Always directed toward the center of the circular path (hence the term “centripetal,” which means center-seeking).
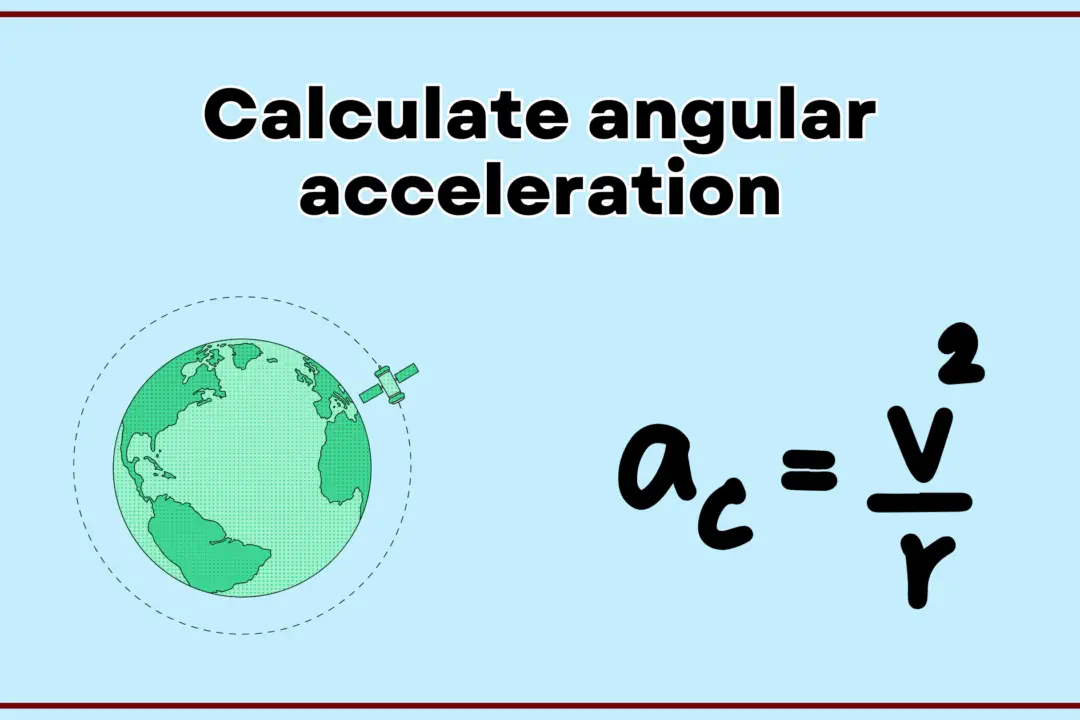
Formula: $a_c = \frac{v^2}{r}$ where $a_c$ is the centripetal acceleration, $v$ is the velocity of the object, and $r$ is the radius of the circular path.
Effect on Motion: It changes the direction of the object’s motion, not its speed.
Example: When a car makes a turn, the friction between the tires and the road provides the centripetal force needed to change the direction of the car. The acceleration toward the center of the curve is centripetal acceleration.

In Calculus Terms:

Linear acceleration is the rate of change of linear velocity. It causes the object to speed up or slow down.
Centripetal acceleration is the rate of change of tangential velocity. It only affects the direction of motion, not the speed.

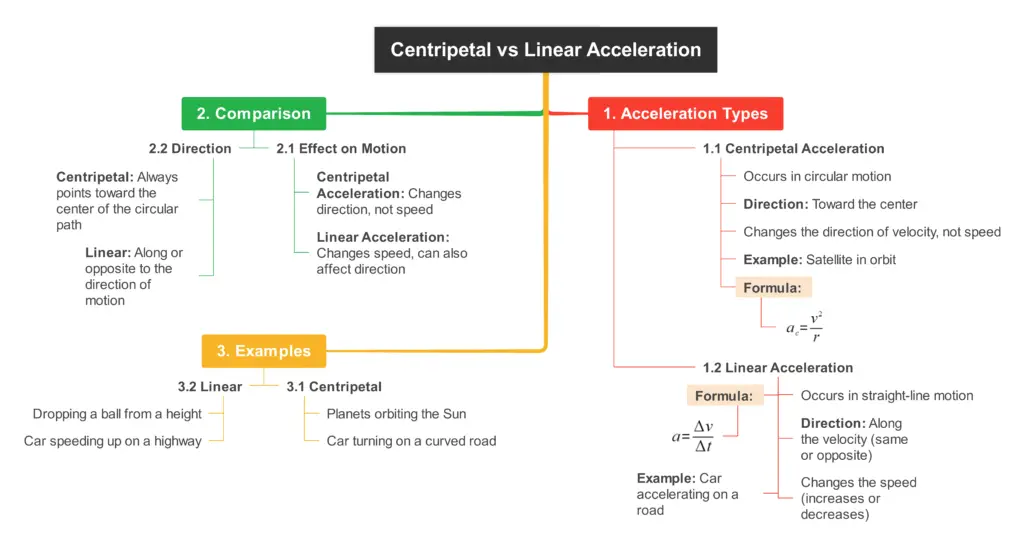
Differences between Centripetal and Linear Acceleration

Direction of Action:
- Linear acceleration acts along the path of motion (tangential to the curve or along a straight line).
- Centripetal acceleration always points toward the center of the circular path and changes the direction of the velocity vector, not its magnitude.
Effect on Motion:
- Linear acceleration changes the magnitude of the velocity (i.e., it speeds up or slows down the object).
- Centripetal acceleration changes only the direction of the object’s motion while maintaining its speed constant.
In a Circular Motion:
- In uniform circular motion, the object experiences centripetal acceleration without any linear (tangential) acceleration if the speed remains constant.
- In non-uniform circular motion, both linear and centripetal accelerations can occur, with linear acceleration affecting the speed and centripetal acceleration affecting the direction.