In this article we will briefly discuss about Coulomb’s Law of Electrostatics. We already know about electric charge and the properties of electric charge. It would be helpful of you revise these concepts before studying about the concept of Coulomb’s Law.
What is Coulomb’s Law?
- Coulomb’s Law is an Inverse-Square Law.
- It describes the force between two electrically charged particles at rest
- It is also known as electrostatic force or Coulomb force
- It was published in 1785 by French physicist Charles-Augustin de Coulomb
Inverse square law force decreases rapidly with increasing distance. This is similar to how gravity operates.
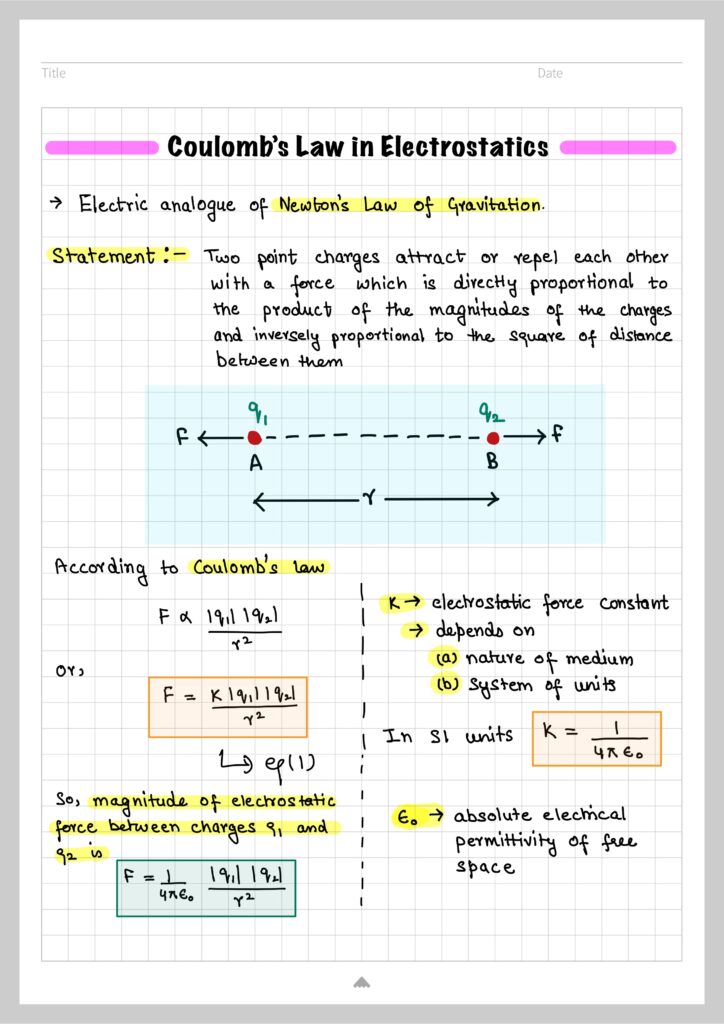
Let us now state coulomb’s law in electrostatics
According to this law, the magnitude of electrostatic force between two point charges is directly proportional to the product of their magnitudes and inversely proportional to the square of distance between them.
- This force could be attractive or repulsive in nature depending on the type of charges involved.
- If both the charges are positive or both the charges are negative then electrostatic force would be repulsive in nature.
- If both the interacting charges are opposite in nature (one negative and one positive) the the force would be attractive in nature.
We have already explained what is coulombs law let us now understand why is it important.
Importance of Coulomb’s Law
Coulomb’s Law is important because:
- It provides a precise way to calculate the force between charged objects.
- It explains the fundamental forces that hold atoms and molecules together.
- It forms the basis for understanding a wide range of electrostatic phenomena.
- It has widespread technological applications in everything from printers to particle accelerators.
Mathematical Expression or Formula
Coulomb’s Law describes the force between two stationary electric charges.
Consider two point charges $q_1$ and $q_2$ kept in vacuum. Let $r$ be the distance between them .
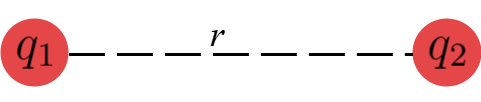
According to Coulomb’s law, the magnitude of electrostatic force between the charges is given by ;
$$F\propto\frac{q_1q_2}{r^2}$$
$$F=k\frac{q_1q_2}{r^2} \tag{1}$$
This equation (1) represents the scalar form of the Coulomb’s Law.
In equation (1) $k$ is a constant of proportionality called electrostatic force constant. The value of $k$ depends on the nature of medium between the two charges and the system of units used.
For charges located in free space (air/vacuum), value of $k$ in SI unit is
$$k=\frac{1}{4\pi\epsilon_0}=\frac{1}{4\pi\times 8.854\times 10^{-12}}=9\times 10^{9}Nm^2/C^2$$
where,
$\epsilon_0=$ Absolute permittivity of free space $=8.854\times 10^{-12} C^2N^{-1}m^{-1}$
Therefore, for vacuum or air, Coulombs law is given by the formula
$$F=\frac{1}{4\pi\times 8.854\times 10^{-12}}\frac{q_1q_2}{r^2} \tag{1}$$
or,
$$F=9\times 10^{9} \times \frac{q_1q_2}{r^2} \tag{2}$$
Above equation (2) gives the magnitude of electrostatic force between two point charges when they are placed in vacuum or air.
Key points to remember:
- The force is directly proportional to the product of the charges $(q_1 \times q_2)$. If you double both charges, the force will quadruple.
- The force is indirectly proportional to the square of the distance $(d^2)$ between the charges. If you double the separation distance, the force will decrease by a factor of four.
Units and Dimensions of $\epsilon_0$
We know that
$$F=\frac{1}{4\pi\times 8.854\times 10^{-12}}\frac{q_1q_2}{r^2} $$
Rearranging this equation for $\epsilon_0$ we get,
$$\epsilon_0=\frac{1}{4\pi\times F}\frac{q_1q_2}{r^2} $$
SI Unit of $\epsilon_0$ as derived from above relation is $C^2N^{-1}m^{-2}$
Dimensions of $\epsilon_0$ :
$$\frac{[AT][AT]}{[MLT^{-2}][L^2]}=[M^{-1}L^{-3}T^4A^2]$$
Summary
Related Articles