In our previous article we have explained about Electric Charge Unit in detail. In this article, we’ll look at the concept of Basic Properties of Electric Charge.
Although we already have a detailed article on the concept of electric charge, let’s start by revising it. So, what is electric charge?
- Electric charge is a fundamental property carried by certain subatomic particles like electrons and protons.
- It governs how these particles interact with electromagnetic fields.
- There are two types of charge: positive (like protons) and negative (like electrons).
Basic Properties of Electric Charges
Electric charge is a scalar quantity that have only magnitude but no direction. There are three fundamental or basic properties of electric charge
- Additivity: Electric charges can be added algebraically, taking into account their positive or negative signs.
- Quantization: Electric charge exists in discrete units, multiples of the elementary charge (e).
- Conservation: The total electric charge within an isolated system remains constant.
In the following sections, we will explore each of these properties in detail.
Additive Nature of Electric Charge
The total electric charge on a body (or system) is equal to the algebraic sum of all the individual electric charges located at different parts of the body (or system).
- Electric charges are additive. This means the total charge of a system is simply the algebraic sum of individual charges within that system.
- For example, if a system has two charges, +3 coulombs (C) and -5 coulombs, the total charge is -2 coulombs.

It is important to note here that, even though we refer to charge as a scalar quantity (only magnitude), it’s crucial to remember that charges have signs – positive (+) or negative (-). The additivity principle takes these signs into account.
Given below are two examples illustrating the additive nature of electric charge:
Example 1:
Imagine three charges placed in a system:
- $q_1 = -4 \, \text{C}$
- $q_2 = +6 \, \text{C}$
- $q_3 = -1 \, \text{C}$
To find the total charge ($Q_{\text{total}}$) of the system, we add these charges together:
$$
Q_{\text{total}} = q_1 + q_2 + q_3 = (-4 \, \text{C}) + (+6 \, \text{C}) + (-1 \, \text{C}) = 1 \, \text{C}
$$
Thus, the system has a total charge of $1 \, \text{C}$.
Example 2:
Consider another system with the following charges:
- $q_1 = +2 \, \text{C}$
- $q_2 = +3 \, \text{C}$
- $q_3 = -5 \, \text{C}$
To calculate the total charge ($Q_{\text{total}}$):
$$
Q_{\text{total}} = q_1 + q_2 + q_3 = (+2 \, \text{C}) + (+3 \, \text{C}) + (-5 \, \text{C}) = 0 \, \text{C}
$$
In this case, the total charge of the system is $0 \, \text{C}$, indicating a neutral system.
Quantization of Electric Charge
The principle of quantization of electric charge states that the charge ($q$) of any object is an integer multiple of the elementary charge ($e$), where $e = 1.6 \times 10^{-19}$ Coulombs. The formula to represent this relationship is:
$$
q = n \cdot e
$$where $n$ is an integer (positive or negative), indicating the number of elementary charges.
- Quantization of charge means that the charge on any object isn’t continuous, but rather exists in discrete “packets” or multiples of a fundamental unit of charge.
- This fundamental unit is called the elementary charge $(e)$, which is the charge carried by a single proton or electron.
- The value of the elementary charge is approximately $e = 1.602 \times 10^{-19}$ Coulombs.
Given below are two examples explaining about the discrete nature or, quantization of electric charge:
Example 1: Proton Charge
A proton has a single positive elementary charge. Thus, for a proton, $n = 1$, making its charge:
$$
q = n \cdot e = 1 \cdot 1.6 \times 10^{-19} \, \text{C} = 1.6 \times 10^{-19} \, \text{C}
$$
Example 2: Charge of an Ion
Consider an ion with a charge equivalent to losing two electrons. Since each electron has a charge of $-1.6 \times 10^{-19}$ C, losing two electrons means the ion has gained a charge of $+2e$. Thus, for this ion, $n = +2$, and its charge is:
$$
q = n \cdot e = 2 \cdot 1.6 \times 10^{-19} \, \text{C} = 3.2 \times 10^{-19} \, \text{C}
$$
Learn more about quantization of charge.
Conservation of Charge
According to law of conservation of electric charges
The total electric charge of an isolated system always remains constant.
This means, within a closed system, charge can be transferred between objects, but it cannot be created out of nothing or simply disappear. The net amount of positive and negative charge in the universe remains constant.
Example illustrating conservation of charge
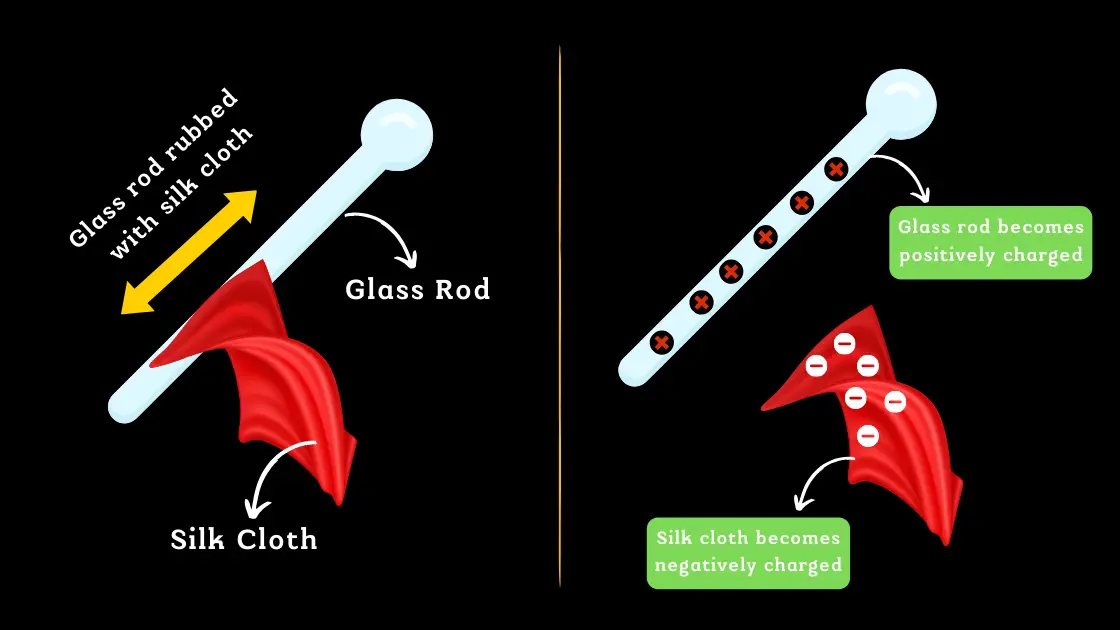
When a glass rod is rubbed with a silk cloth, there is a transfer of electrons from the silk to the glass rod. This transfer of electrons results in the glass rod becoming positively charged, while the silk cloth becomes negatively charged.
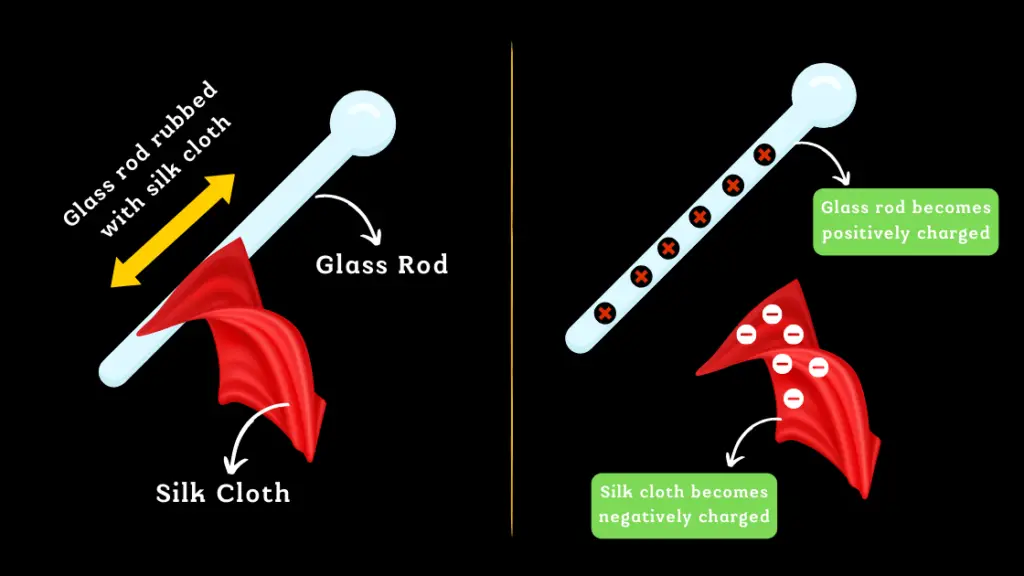
Although the glass rod and silk cloth now have opposite charges, the total charge of the system remains zero, as the amount of positive charge on the glass rod is equal to the amount of negative charge on the silk cloth.
It’s important to note that rubbing the glass rod with the silk cloth doesn’t create new charges, it only redistributes the existing charges. The positive charge on the glass rod is balanced by the negative charge on the silk cloth, and vice versa.
This demonstrates the principle of charge conservation, which states that the total electric charge of an isolated system remains constant, regardless of any interactions that may occur within the system. The transfer of charge between the glass rod and the silk cloth does not create or destroy charge, it only redistributes it.
Summary
| Property | Description |
|---|---|
| Like charges repel each other | Two objects with the same charge will push each other away |
| Unlike charges attract each other | Two objects with different charges will pull each other together |
| Quantization of charge | Charge is not continuous, it comes in discrete packets, or quanta |
| Magnitude of charge is independent of speed | The charge on an object does not change with its motion |
| Electric charge is a scalar quantity | Charge is a measure of the amount of electric charge an object contains |
| Conservation of electric charge | The total electric charge of an isolated system remains constant over time |
| Electric charge is a fundamental property of matter | Charge is an intrinsic property of particles and objects, and it cannot be created or destroyed |
| Electric charge is a universal force | Electric charge acts between charged objects, regardless of their size, shape, or distance |