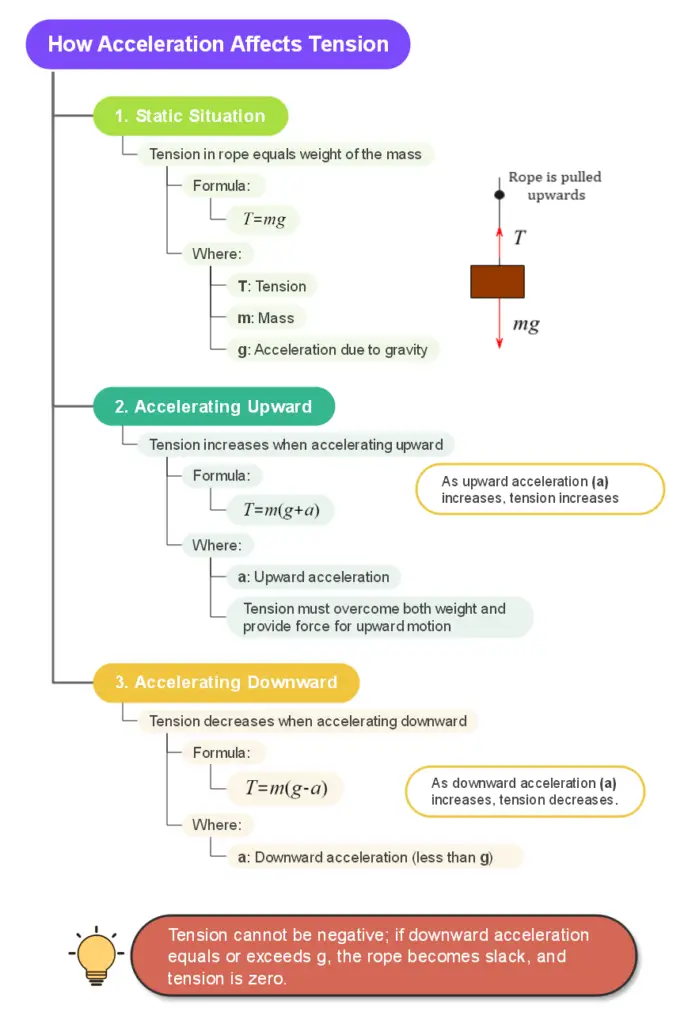
Acceleration directly affects tension in a system by increasing or decreasing the force required to change an object’s velocity. As acceleration increases, tension generally increases, and as acceleration decreases, tension typically decreases.
Explanation
To understand how acceleration affects tension, let’s consider a simple scenario: a mass hanging from a rope that is being pulled upward.
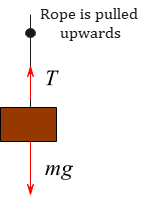
Static situation: When the mass is at rest or moving at constant velocity, the tension in the rope is equal to the weight of the mass:
$T = mg$
Where:
- $T$ is tension
- $m$ is mass
- $g$ is acceleration due to gravity
Accelerating upward: If the rope is pulled upward, causing the mass to accelerate, the tension in the rope increases:
$T = m(g + a)$
Where:
- $a$ is the upward acceleration In this case, the tension must overcome both the weight of the mass and provide the force needed for upward acceleration.
Accelerating downward: If the mass is allowed to fall with an acceleration less than $g$, the tension in the rope decreases:
$T = m(g – a)$
Where:
- $a$ is the downward acceleration (less than $g$)
The relationship between acceleration and tension can be understood through Newton’s Second Law of Motion:
$F = ma$
In a tension scenario, the net force $(F)$ is the difference between tension and weight:
$T – mg = ma$
Rearranging this equation gives us:
$T = m(g + a)$
This formula clearly shows how acceleration directly influences tension. As acceleration $(a)$ increases in the positive direction (upward), tension increases. Conversely, as acceleration increases in the negative direction (downward), tension decreases.
It’s important to note that tension cannot be negative in real-world scenarios. If the downward acceleration equals or exceeds $g$, the rope becomes slack, and tension effectively becomes zero.
Understanding this relationship is crucial in various applications, from designing elevator systems to analyzing forces in pendulums and other dynamic systems involving ropes or cables.