Point Object in Physics
In physics, we often simplify complex systems by considering objects as point particles or point objects. A point object, also known as a particle, is an object that can be mathematically represented as a single point in space. This is an idealized concept, as in reality, all objects have a finite size. However, this simplification is useful in many physical situations and allows us to apply the laws of physics more easily.
Definition of a point object
A point object is an object whose entire mass is concentrated at a single point in space.
In other words, we can consider an object as a point object if the distance covered by the object is significantly larger than its own dimensions.
This means that the size, shape, and structure of the object are not considered in the analysis of its motion or other physical properties.
Examples of point objects in physics
The concept of a point object is widely used in physics, especially in mechanics. For example, when studying the motion of a car moving along a straight road, we can consider the car as a point object. This is because the dimensions of the car are negligible compared to the distance it travels.
Similarly, when we study the motion of planets around the Sun, we consider the planets and the Sun as point objects. This is because the distances between them are much larger than their own sizes.
Mathematical representation
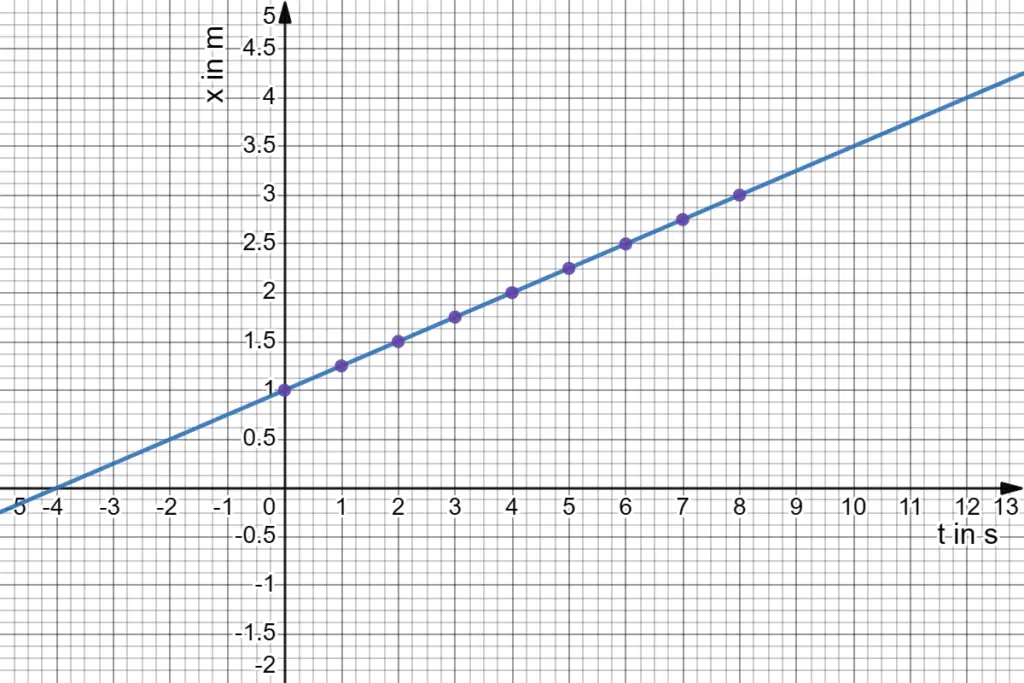
In physics, a point object is often represented by a dot in a diagram or a set of coordinates in a mathematical equation. For example, if we consider a point object moving in a straight line, its position can be represented by a single coordinate (x) in one-dimensional motion. In two-dimensional motion, two coordinates (x, y) are used, and in three-dimensional motion, three coordinates (x, y, z) are used.
Criteria for considering an object as a point
In physics, an object can be considered as a point object when its size is negligible compared to the distance it covers during its motion. This simplification allows us to focus on the object’s overall motion, ignoring the details of its size and shape. Examples include a car moving on a long road or a planet orbiting the Sun, where their dimensions are small compared to the distances involved.

Limitations
While the concept of a point object simplifies many problems in physics, it has its limitations. It cannot be used when the size, shape, or structure of the object is important. For example, in cases where the rotation of an object is considered, or when the internal structure of an object affects its behaviour, the point object approximation is not valid.
Formulas
The motion of a point object can be described using the following formulas:
1. For linear motion with constant acceleration (a), the final velocity (v) of the object after time (t) is given by:
\(v = u + at\)
where u is the initial velocity.
2. The displacement (s) of the object in time (t) is given by:
\(s = ut + \frac{1}{2}at^2\)
3. For an object moving in a circular path with a constant speed (v) and radius (r), the centripetal acceleration (a) is given by:
\(a = \frac{v^2}{r}\)
Remember, these formulas are applicable when we consider the object as a point object.
Review Questions
1. What is a point object in physics? When can an object be considered a point object?
2. How is a point object represented mathematically in one-dimensional, two-dimensional, and three-dimensional motion?
3. What are the limitations of considering an object as a point object in physics?
Answer
1. A point object in physics, also known as a particle, is an object whose entire mass is concentrated at a single point in space. The size, shape, and structure of the object are not considered in the analysis of its motion or other physical properties. An object can be considered as a point object if the distance covered by the object is significantly larger than its own dimensions. For example, when studying the motion of a car moving along a straight road, we can consider the car as a point object because the dimensions of the car are negligible compared to the distance it travels.
2. A point object is represented mathematically by a set of coordinates. In one-dimensional motion, its position can be represented by a single coordinate (x). In two-dimensional motion, two coordinates (x, y) are used, and in three-dimensional motion, three coordinates (x, y, z) are used.
3. The concept of a point object has its limitations. It cannot be used when the size, shape, or structure of the object is important. For example, in cases where the rotation of an object is considered, or when the internal structure of an object affects its behaviour, the point object approximation is not valid.
Further Reading
For more details on point objects and their applications in physics, you can refer to the following links:
1. Mechanical Motion
2. Reference frame
3. Isotropy and Uniformity in Space