Acceleration can change with time in various ways, depending on the forces acting on an object and the specific situation. The relationship between acceleration and time is not always constant and can be described by different mathematical functions.
How does acceleration change with time?
To understand how acceleration changes with time, we need to consider the following concepts:
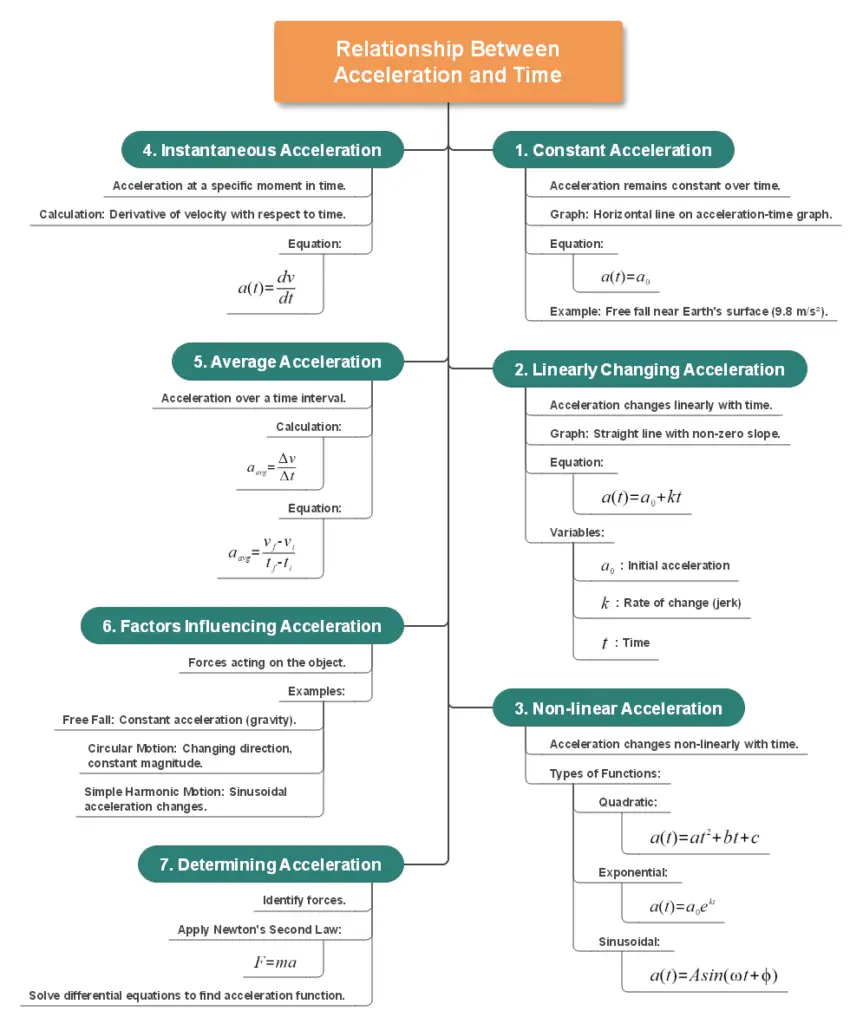
- Constant acceleration: In some cases, acceleration remains constant over time. This is represented by a straight horizontal line on an acceleration-time graph. The equation for constant acceleration is: $a(t) = a_0$ Where $a_0$ is the constant acceleration value.
- Linearly changing acceleration: Acceleration can change linearly with time, resulting in a straight line with a non-zero slope on an acceleration-time graph. This is described by the equation: $a(t) = a_0 + kt$ Where $a_0$ is the initial acceleration, $k$ is the rate of change of acceleration (jerk), and $t$ is time.
- Non-linear acceleration: In more complex situations, acceleration can change non-linearly with time. This can be represented by various functions, such as quadratic, exponential, or sinusoidal equations. For example: Quadratic: $a(t) = at^2 + bt + c$
Exponential: $a(t) = a_0e^{kt}$
Sinusoidal: $a(t) = A\sin(\omega t + \phi)$ - Instantaneous acceleration: The instantaneous acceleration at any given time can be calculated by taking the derivative of the velocity function with respect to time: $a(t) = \frac{dv}{dt}$
- Average acceleration: The average acceleration over a time interval can be calculated using: $a_{avg} = \frac{\Delta v}{\Delta t} = \frac{v_f – v_i}{t_f – t_i}$
The way acceleration changes with time depends on the forces acting on the object. For example:
- In free fall near Earth’s surface, acceleration due to gravity is approximately constant (9.8 m/s²).
- In circular motion, the acceleration vector changes direction continuously, even if its magnitude remains constant.
- In simple harmonic motion, acceleration changes sinusoidally with time.
To determine how acceleration changes with time in a specific situation, we need to:
- Identify the forces acting on the object
- Apply Newton’s Second Law of Motion: $F = ma$
- Solve the resulting differential equations to find the acceleration function
Understanding how acceleration changes with time is crucial for analyzing and predicting the motion of objects in various physical systems, from simple projectile motion to complex orbital dynamics.
Mind Map on relation between acceleration and time