In our previous article we learned about Coulomb’s Law of electrostatics. In this article, we will learn about the concept of permittivity and relative permittivity and how it affects the force between charged particles.
When charges are placed in a medium other than a vacuum, the force between them changes due to the relative permittivity of that medium.
For example, when charges are placed in water instead of air/vacuum, the force between them decreases by a factor of about 80, since the relative permittivity of water is around 80.
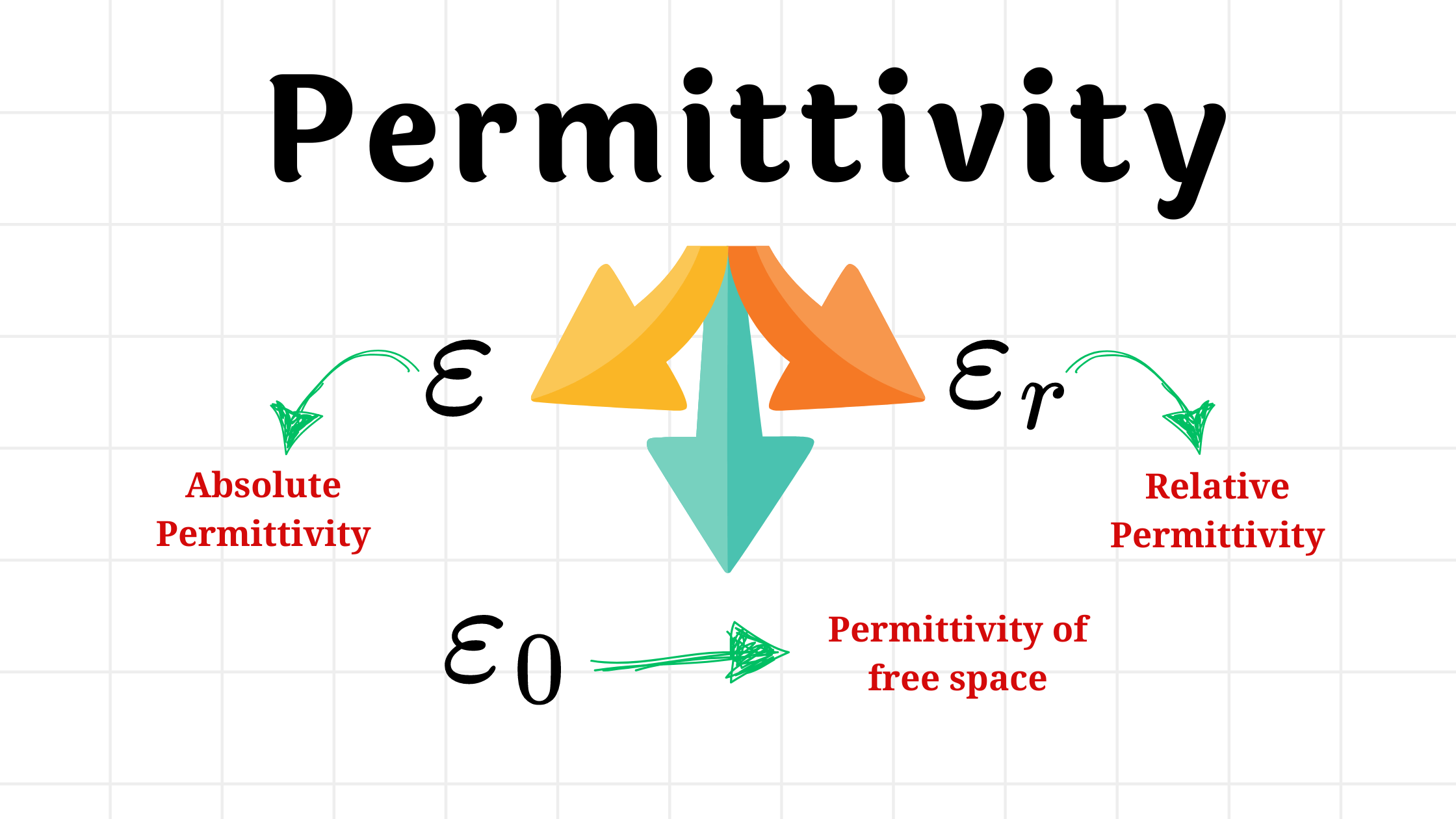
What is Permittivity?
Permittivity is a measure of how much the force between charged particles changes when they are moved from a vacuum to another medium.
We can also explain this in terms of electric field. Permittivity, symbolized by $\epsilon$, is a characteristic of materials indicating their responsiveness to electric fields. It measures how easily electric fields can penetrate a substance and influence the strength of the electric force between charged particles within it.
Essentially, permittivity reflects how well a material allows electric fields to pass through it. It is denoted by epsilon $\epsilon$.
The permittivity of a vacuum or free space is denoted by $\epsilon_0$ and has a value of $8.85 \times 10^{-12} C^2/Nm^2$. It serves as a reference point for comparing the permittivity of other materials.
What is Relative Permittivity?
The relative permittivity $(\epsilon_r)$ is the ratio of the permittivity of a medium to the permittivity of a vacuum. It is a comparison between the permittivity of the medium and that of the vacuum.
For example, the relative permittivity of water is 80, which means that the permittivity of water is 80 times that of the vacuum. Let us understand this with the help of electrostatic force as defined by Coulomb’s Law.
The formula for the force between charged particles in a vacuum or air is:
$$F_{vac}=\frac{1}{4\pi\epsilon_0}\frac{q_1q_2}{r^2}\tag{1}$$
where $q_1$ and $q_2$ are the charges and $r$ is the distance between them and $\epsilon_0$ is the permittivity of free space.
The formula below describes the force between two charged particles with charges $q_1$ and $q_2$, separated by a distance $r$, in a medium characterized by absolute permittivity $\epsilon$:
$$F_{med}=\frac{1}{4\pi\epsilon}\frac{q_1q_2}{r^2}\tag{2}$$
Now dividing equation (1) by (2) we get
$$\frac{F_{vac}}{F_{med}}=\frac{\frac{1}{4\pi\epsilon_0}\frac{q_1q_2}{r^2}}{\frac{1}{4\pi\epsilon}\frac{q_1q_2}{r^2}}=\frac{\epsilon}{\epsilon_0}\tag{3}$$
The ratio $\frac{\epsilon}{\epsilon_0}$ is denoted by $\epsilon_r$, called relative permittivity of the medium w.r.t. vacuum. It is also denoted by $K$, called dielectric constant of the medium. So, equation (3)
$$\epsilon_{r}\text{ (or K)}= \frac{\epsilon}{\epsilon_0}=\frac{F_{vac}}{F_{med}}\tag{4}$$
Above equation (4) gives relative permittivity formula.
From above equation we can say that
Relative permittivity or dielectric constant of a medium may be defined as the ratio of the force between two charges placed at a certain distance apart in air to the force between the same charges placed at the same distance apart in that medium.
How Permittivity Affects the Force
The value of $\epsilon$ affects the force between charged particles. When the value of $\epsilon$ increases, the force decreases, and when the value of ε decreases, the force increases.
Conclusion
To put it simply, permittivity is a measure of how much the force between charged particles changes when they are transferred from a vacuum to another medium.
The relative permittivity is defined as the ratio of a medium’s permittivity to that of a vacuum.
Understanding permittivity and relative permittivity is important for understanding the behaviour of charged particles in different mediums.