We already know about vectors and scalars in physics. In this article, we will explore how to represent vectors graphically.
Now we already know vectors have
- Magnitude and
- Direction
To represent them graphically we must take account of both magnitude and direction of a vector quantity.
How to represent vectors graphically?
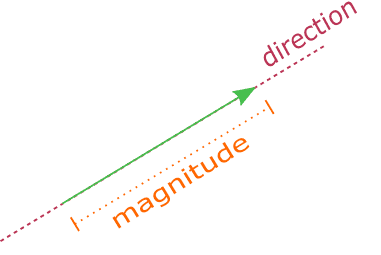
Vectors are represented graphically by directed line segments.
They are represented such that the length of the line segment is the magnitude of the vector and the direction of the arrow marked at one end represents the direction of the vector.
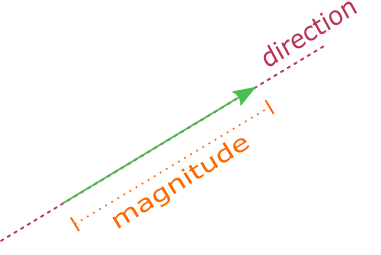
The length of the line shows the magnitude or size of the vector and the direction of the arrowhead shows the direction of the vector.
The starting point of the vector is called the “tail” of the vector and its ending point is known as “head” of the vector.

In this figure point, \(A\) is the initial point or tail of the vector, and \(B\) is called the terminal point, tip, or head of the vector.
This directed line segment with its tail at point A and head at point B is written as \(\vec{AB}\) or AB. So, vectors are also represented symbolically either by the arrow on top of the symbol or in bold type.
Here in this figure shown above \(\vec a =\vec{AB}\). The magnitude of this vector is \[\left|\vec{a}\right|=\left|\vec{AB}\right|=AB\]
which is the distance between the head and tail of the vector.
It must be noted that the magnitude of a vector is always a non-negative real number.
Every vector has the following three characteristics
Length of the vector:
The length of the vector \(\vec a =\vec{AB}\) is denoted by \(\left|\vec{AB}\right|=AB\)
Support of the vector:
The line of unlimited length of which \(AB\) is a segment is called the support of the vector \(\vec{AB}\).
Sense:
The sense of the vector \(\vec{AB}\) is from point \(A\) to point \(B\) and the sense of the vector \(\vec{BA}\) is from \(B\) to \(A\). The sense of ant vector is from its initial point to its final point.
Further Reading