The spherical coordinate system is a three-dimensional coordinate system used extensively in fields like physics, mathematics, and engineering.
What is a Spherical Coordinate System?
The spherical coordinate system defines a point in three-dimensional space using three coordinates:
- radial distance (r),
- polar angle (θ), and
- azimuthal angle (φ)
The radial distance is the distance from the origin, the polar angle is measured from the z-axis, and the azimuthal angle is measured in the xy-plane.
For a broader understanding of coordinates, you may refer to What are Coordinates in Physics.
Coordinates Definition
The diagram given below represents the spherical coordinate system, clearly showing the radial distance, polar angle, and azimuthal angle for a point $P$ in three-dimensional space.
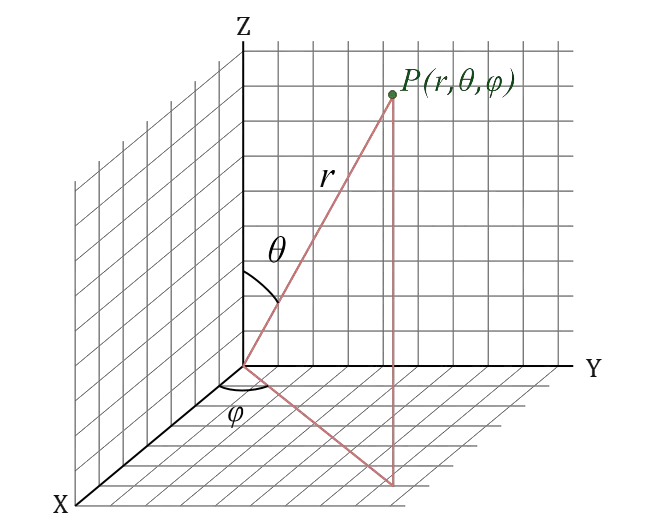
Radial Distance ($r$):
The radial distance is the straight-line distance from a point to the origin of the coordinate system. In the spherical coordinate system, it represents how far a point is from the center or origin, without regard to the direction in which it lies.
Polar Angle ($\theta$):
The polar angle, often denoted by the Greek letter theta ($\theta$), is the angle between the radial line connecting a point to the origin and the positive z-axis. It is measured in radians or degrees and ranges from 0 to $\pi$ radians (or 0 to 180°).
Azimuthal Angle ($\phi$):
The azimuthal angle is commonly represented by the Greek letter phi ($\phi$). It is the angle between the projection of the radial line on the xy-plane and the positive x-axis. It also is measured in radians or degrees and ranges from 0 to $2\pi$ radians (or 0 to 360°).
The azimuthal angle helps identify the direction of a point in the flat xy-plane, much like how longitude helps you find a specific location east or west on a map of the Earth.
Converting from spherical to cartesian coordinates
Converting from spherical coordinates to Cartesian coordinates involves translating a point defined by radial distance, and two angles (polar and azimuthal) to one described by three perpendicular axes (x, y, z). Here’s how you can perform this conversion:
Given a point in $P$ in spherical coordinates \((r, \theta, \phi)\), the conversion to Cartesian coordinates \((x, y, z)\) is done as follows:
1. x-coordinate: The x-coordinate can be found using the radial distance, polar angle, and azimuthal angle:
\[
x = r \sin \theta \cos \phi
\]
2. y-coordinate: The y-coordinate is determined similarly, incorporating the same spherical coordinates:
\[
y = r \sin \theta \sin \phi
\]
3. z-coordinate: The z-coordinate uses the radial distance and polar angle:
\[
z = r \cos \theta
\]
Converting from cartesian to coordinates spherical
The conversion from Cartesian coordinates to spherical coordinates involves the transition from using three perpendicular axes (x, y, z) to using radial distance, and two angles (polar and azimuthal) to describe a point in space. Here’s how you can convert from Cartesian to spherical coordinates:
Given a point in Cartesian coordinates \((x, y, z)\), the conversion to spherical coordinates \((r, \theta, \phi)\) is done as follows:
1. Radial Distance (r): This is the distance from the origin to the point. It can be found using the Pythagorean theorem:
\[
r = \sqrt{x^2 + y^2 + z^2}
\]
2. Polar Angle (\(\theta\)): This angle is measured from the positive z-axis to the radial line connecting the origin to the point. It can be found using the arccosine function:
\[
\theta = \arccos\left(\frac{z}{r}\right) = \arccos\left(\frac{z}{\sqrt{x^2 + y^2 + z^2}}\right)
\]
3. Azimuthal Angle (\(\phi\)): This angle defines the direction of the point in the xy-plane, much like longitude on a map. It can be found using the arctangent function:
\[
\phi = \arctan\left(\frac{y}{x}\right)
\]
These equations enable the transformation from the familiar Cartesian coordinates to the spherical coordinates, which can be particularly useful in physics and mathematics when dealing with problems involving spherical symmetry.
Unit vectors in spherical coordinate system
In the spherical coordinate system, the unit vectors are not constant in all directions as they are in the Cartesian coordinate system. They change direction depending on the point, and they are defined as follows:
1. Radial Unit Vector \(\hat{r}\): Points in the direction of increasing radial distance \(r\) and is tangent to the sphere with radius \(r\). It’s directed away from the origin, aligned with the radius.
2. Polar Unit Vector \(\hat{\theta}\): Points in the direction of increasing polar angle \(\theta\) and is tangent to the sphere defined by the particular polar angle. It’s directed downward in the spherical coordinate system.
3. Azimuthal Unit Vector \(\hat{\phi}\): Points in the direction of increasing azimuthal angle \(\phi\) and is tangent to the circle defined by a particular azimuthal angle. It’s directed counter-clockwise in the xy-plane, perpendicular to both \(\hat{r}\) and \(\hat{\theta}\).
Mathematical Definitions
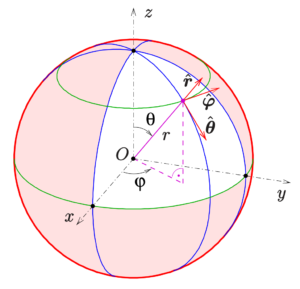
The unit vectors can be expressed in Cartesian coordinates as:
\[
\begin{align*}
\hat{r} & = \sin \theta \cos \phi \, \hat{i} + \sin \theta \sin \phi \, \hat{j} + \cos \theta \, \hat{k} \\
\hat{\theta} & = \cos \theta \cos \phi \, \hat{i} + \cos \theta \sin \phi \, \hat{j} – \sin \theta \, \hat{k} \\
\hat{\phi} & = -\sin \phi \, \hat{i} + \cos \phi \, \hat{j}
\end{align*}
\]
Orthogonality of unit vectors
The unit vectors in the spherical coordinate system are orthogonal to each other at any given point. Being orthogonal means that they are mutually perpendicular, forming right angles with each other.
- The radial unit vector \(\hat{r}\) is orthogonal to both the polar unit vector \(\hat{\theta}\) and the azimuthal unit vector \(\hat{\phi}\).
- The polar unit vector \(\hat{\theta}\) is orthogonal to both the radial unit vector \(\hat{r}\) and the azimuthal unit vector \(\hat{\phi}\).
- The azimuthal unit vector \(\hat{\phi}\) is orthogonal to both the radial unit vector \(\hat{r}\) and the polar unit vector \(\hat{\theta}\).
This orthogonality is fundamental to the structure of the spherical coordinate system. By defining these three unit vectors that are perpendicular to each other, we create a basis that can describe any vector in the three-dimensional space in terms of its spherical coordinates. It is similar in function to the \(i\), \(j\), and \(k\) unit vectors in the Cartesian coordinate system but takes into account the spherical geometry.