How to find vector components from magnitude and angle

We already know what are vectors in physics and How to represent vectors graphically. In this article, we will look at the way to find vector components from magnitude and angle.

Finding vector components from magnitude and angle

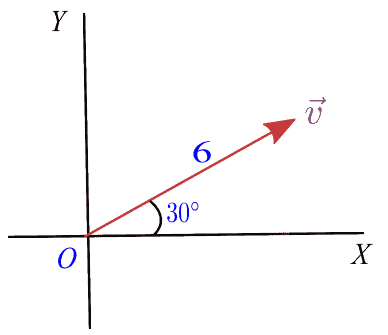
Let us proceed further with a problem which is how to find the components of a vector given magnitude and angle. So our problem is to 

find the components of a vector $\vec{v}$ which has a magnitude of 6 units and is directed at an angle of $30^{\circ}$ with respect to the x-axis. 

Let us now represent our vector graphically from the information given in the problem.

This vector $\vec{v}$ can be represented by the hypotenuse of this triangle shown below in the figure. 

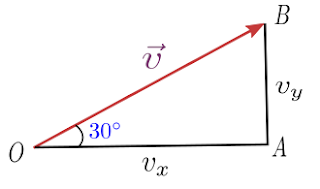
Here $OA=v_x$ represent the x component and $AB=v_y$ represent the y component of the vector $\vec{v}$. In terms of components vector v is written as 

$\vec{v}=v_x\hat{i}+ v_y\hat{j}$ 

where $\hat{i}$ and $\hat{j}$ are the unit vectors along x and y axis respectively. 

From trigonometry we know that for any right angled triangle with hypotenuse (H), base (B) and perpendicular (P) 

$\sin\theta=\frac{perpendicular}{hypotenuse}$ 

$\cos\theta=\frac{base}{hypotenuse}$ 

where $\theta$ is the angle between base and hypotenuse. 

Now since triangle $OAB$ is a right angled triangle with 

 $Base=OA=v_x$ 

$Hypotenuse=OB=|\vec{v}|$ and 

$Perpendicular=AB=v_y$ 

We have, 

$v_x=|\vec{v}|\cos\theta$ and 

$v_y=|\vec{v}|\sin\theta$ 

Here $|\vec{v}|$ is the magnitude of the vector $\vec{v}$. 

From our problem $|\vec{v}|=6$ and $\theta=30^{\circ}$ so, we have 

$v_x=6\cos30^{\circ}$ $v_y=6\sin30^{\circ}$ 

Again from trigonometry 

 $\cos30^{\circ}=frac{\sqrt{3}}{2}$ 

and 

$\sin30^{\circ}=\frac{1}{2}$ 

Which gives us 

$v_x=6\times \frac{\sqrt{3}}{2}=3\sqrt{3}$ 

and 

$v_y=6\times \frac{1}{2}=3$ 

So,  $(3\sqrt{3},3)$ are the vector components that we have found when we are given the information about magnitude and angle of the vector.

You can verify this answer by finding the magnitude of the vector using the components of the vector we have calculated. This can be done by using Pythagoras theorem for where you are finding the hypotenuse of triangle $OAB$ which is nothing but magnitude of our vector in question.

Let us look at our another solved example where we would find vector components from magnitude and direction.

Solved Example 

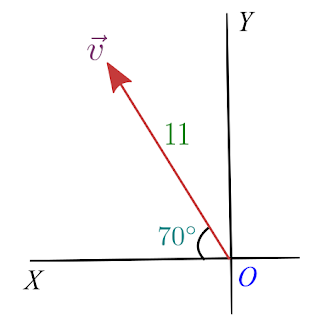
 In the vector $\vec{v}$ as shown below in the figure convert vector from magnitude and direction form into component form.

Solution 

Here it is given in the question that magnitude of $\vec{v}$ is $11$ and the angle vector makes with the x-axis is $70^{\circ}$. This vector $\vec{v}$ can be represented by the hypotenuse of this triangle shown below in the figure.

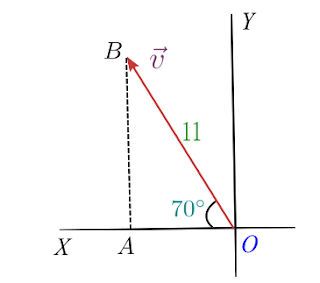
Finding x component of $vec{v}$ 

$v_x=-|\vec{v}|\cos\theta  = -11\ cos (70^{\circ}) \approx -3.76$

Here negative sign appears because our vector is in the second quadrant where all values of x are negative as can be seen clearly from the figure and values of y are all positive. 

Finding y component of $\vec{v}$ 

$v_y=|\vec{v}|\sin\theta  = 11 \sin (70^{\circ}) \approx 10.34$ 

Our answer is

$\vec{v}\approx \left(-3.76,10.34 \right)$

Similarly you can find the vector components from magnitude and angle even if vector lie in third or fourth quadrant.

Questions and Answers

Further Reading 

1. https://www.grc.nasa.gov/www/k-12/airplane/vectors.html
2. https://www.physicsclassroom.com/class/1DKin/Lesson-1/Scalars-and-Vectors