Spherical to Cartesian coordinates conversion is the topic we will be studying in this article. In physics and mathematics, coordinate systems are essential for describing the position of points in a space. Two commonly used coordinate systems are Cartesian and Spherical.
Cartesian coordinates \((x, y, z)\) are straightforward and are often the first system students learn. Spherical coordinates \((r, \theta, \phi)\), on the other hand, are particularly useful when dealing with problems that have spherical symmetry.
Conversion from Spherical to Cartesian Coordinates
In physics and mathematics, coordinate systems are essential for describing the position of points in a space. Two commonly used coordinate systems are Cartesian and Spherical.
Cartesian coordinates \((x, y, z)\) are straightforward and are often the first system students learn. Spherical coordinates \((r, \theta, \phi)\), on the other hand, are particularly useful when dealing with problems that have spherical symmetry.
In this article, we will focus on converting points from spherical to Cartesian coordinates.
Cartesian Coordinates
In a Cartesian coordinate system, a point \(P\) in space is defined by three coordinates \((x, y, z)\), where \(x\), \(y\), and \(z\) are the distances of the point from the origin along the \(x\), \(y\), and \(z\)-axes, respectively.
Spherical Coordinates
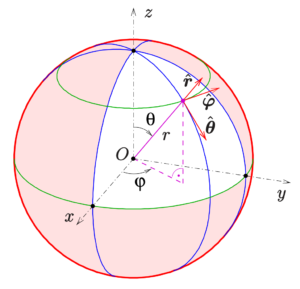
In a spherical coordinate system, a point \(P\) is defined by three coordinates \((r, \theta, \phi)\), where:
- \(r\) is the distance from the origin to the point \(P\).
- \(\theta\) is the angle between the positive \(x\)-axis and the projection of the line segment \(OP\) onto the \(xy\)-plane.
- \(\phi\) is the angle between the positive \(z\)-axis and the line segment \(OP\).
Spherical to Cartesian Coordinates Conversion Formulas
To convert a point from spherical coordinates \((r, \theta, \phi)\) to Cartesian coordinates \((x, y, z)\), the following formulas are used:
\[
x = r \sin \phi \cos \theta
\]
\[
y = r \sin \phi \sin \theta
\]
\[
z = r \cos \phi
\]
Solved Example on Spherical to Cartesian coordinates conversion
Let’s consider a point \(P\) with spherical coordinates \((r = 5, \theta = \frac{\pi}{4}, \phi = \frac{\pi}{3})\).
Using the conversion formulas, we get:
\[
x = 5 \sin \left(\frac{\pi}{3}\right) \cos \left(\frac{\pi}{4}\right) \approx 3.54
\]
\[
y = 5 \sin \left(\frac{\pi}{3}\right) \sin \left(\frac{\pi}{4}\right) \approx 3.54
\]
\[
z = 5 \cos \left(\frac{\pi}{3}\right) \approx 2.5
\]
So, the Cartesian coordinates of the point \(P\) are approximately \((3.54, 3.54, 2.5)\).
Related Questions and Answers
Q: Can these formulas be used in all quadrants?
Answer: Yes, these formulas are valid in all quadrants and octants of the Cartesian coordinate system.
Q: What are the limitations of spherical coordinates?
Answer: Spherical coordinates are less intuitive for problems that lack spherical or radial symmetry.
Q: How do you convert from Cartesian to Spherical coordinates?
Answer: To convert from Cartesian to Spherical coordinates, use the formulas \( r = \sqrt{x^2 + y^2 + z^2} \), \( \theta = \arctan2(y, x) \), and \( \phi = \arccos\left(\frac{z}{r}\right) \). These equations map \((x, y, z)\) to \((r, \theta, \phi)\).
By understanding these conversions, you can easily switch between Cartesian and Spherical coordinate systems, which is a crucial skill in fields like physics, engineering, and computer graphics.