The concept of work done is fundamental in physics. Whether you are studying physics as a pastime or preparing for tests such as the MCAT, AP Physics, GCSE, or IB, you must track your progress.
You can test your concepts in this Work done quiz by taking this online practice quiz. Concepts you must be comfortable with before taking this quiz are
- Motion (Kinematics 1D and 2D)
- Force
- Work Done and
- work energy theorem
This quiz only includes algebra-based questions on the concept of work.
Work Done Quiz Questions and Answers
Question 1 Product of force and displacement is called
(a) work done
(b) energy
(c) acceleration
(d) power
Answer
(a)
Question 2 What is the metric unit of work?
(a) meter
(b) Joule
(c) Watt
(d) horsepower
Answer
(b)
Question 3 Calculate the work done in moving a block of 15 Kg by a distance of 4 m when 50 N of force is being applied to it.
(a) 200 Joules
(b) 2000 Joules
(c) 300 Joules
(d) 3000 Joules
Answer
(a)
Work done, $W= F\times d = 50\times 4=200Joules$
It is important to note that when we are calculating work, the mass of the object that is being displaced is irrelevant.
Question 4 Consider the diagram below, which depicts a force of $10N$ being applied to a box of mass $20 Kg$ at an angle of $60^0$. This force moves the box $20m$ across the smooth table horizontally. The work done by the force is
(a) 100 J
(b) 150 J
(c) 10 J
(d) 200 J
Answer
(a)
From the figure, we can see that force is acting at an angle of 60 degrees with the direction of the displacement. Here force would have two components
- x-axis
- y-axis
The component of force along the y-axis does not contribute to the work done by the force. Only a component of force along the direction of displacement is effective. So we have,
$W=(F\cos\theta)d$
The force is applied at a $60$ angle from the direction of displacement, so $\theta = 60^0$
$W=(F\cos\theta)d$
$W=(10N)(\cos60^0)(20m)=(10N)(0.5)(20m)$
$W=100J$
Question 5 A porter lifts a 15 Kg box from the ground to a height of 2.0 m. The work done by the porter on the box would be equal. ($g=9.8 m/s^2$)
(a) 300 N
(b) 290 N
(c) 294 N
(d) 297 N
Answer
(c)
It is given in the question that
$m=15 Kg$; $distance\;\;s= 2.0m$ ; $g=9.8 m/s^2$ and we have to calculate work $W=?$
Now, Force applied $=F=mg$ (weight of the box)
$F=15Kg\times9.8m/s^2=147N$
Work done $W=F\cdot s=147N\cdot 2.0 m = 294N$
Question 6 Work is done on a body when
a. A force acts on the body, but the body is not displaced.
b. Force does not act on the body, but it is displaced.
c. Force acts on the body in the direction perpendicular to the direction of the displacement of the body.
d. Force acts on the body and the body is either displaced in the direction of force or opposite to the direction of the force.
Answer
(d)
We know that work done,
$W=F\cdot s=Fs\cos\theta$
When the force and displacement are both in the same direction, $theta = 0$. As a result, the work done would be
$W=Fs\cos0^0 = FS$
in a case when force and displacement happen to be opposite to each other $\theta = 180^0$. So, the work done would be
$W=Fs\cos180^0=-Fs$
This is the case of negative work done. The work done by frictional force when pushing a block on a hard surface is an example of negative work.
Question 7 In case of negative work, the angle between force and displacement is
a. $0^0$
b. $45^0$
c. $90^0$
d. $180^0$
Answer
(d)
Question 8. In a tug of war, work done by a winning team is
a. zero
b. positive
d. negative
d. none of these
Answer
(b)
Work done by the winning team is positive because
- In a tug of war, the winning team exerts a force on the opposing team and successfully moves it over a distance.
- The losing team goes toward the winning team as the winning team tugs the rope in its direction.
- Because the applied force is in the same direction as the motion, the work done is positive.
Question 9. What is the work done by gravity if a 90 kg block is pushed along a 100 m track?
a. 10 J
b. 0 J
c. 90 J
d. 100 J
Answer
(b)
The work done by any force that is perpendicular to the direction of displacement is equal to zero.
Question 10. A child builds a tower from three blocks. The blocks are uniform cubes of side 2 cm. The blocks are initially all lying on the same horizontal surface, and each block has a mass of 0.1 kg. The work done by the child is
(a) 4J
(b) 0.04 J
(c) 6J
(d) 0.06 J
Answer
(d)
It is given in the question that
The blocks are uniform cubes of side =2 cm = .02 m
Mass of block $0.1 Kg$
Total work done is a change in kinetic energy plus the change in potential energy. Since the change in kinetic energy is zero. So the total work done by the child would be equal to the total change in the potential energy of blocks.
Potential Energy $=mg\Delta h$
Potential Energy of block 1 $=0.1 \times 10 \times 0$
Potential Energy of block 2 $=0.1 \times 10 \times .02 = 0.02 J$
Potential Energy of block 3 $=0.1 \times 10 \times .02 = 0.04 J$
Thus, the total potential energy is,
$P.E. = 0+0.02+0.04=0.06 J$
Question 11. A certain force acting on a body of mass 2 kg increases its velocity from 6 m/s to 15 m/s in 2 s. The work done by the force during this interval is
a. 27 J
b. 3 J
c. 94.5 J
d. 189 J
Answer
(d)
we know that
$v=u+at$
$15=6+a(2)$
$a=4.5m/s^2$
$s=ut+\frac{1}{2}at^2=6(2)+0.5(4.5)(4)=21m$
$W=F\cdot s=2(4.5)(21)=189J$
Question 12 In which of the following cases work done would be maximum
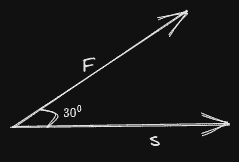
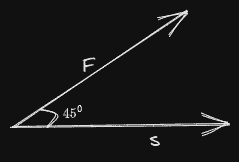
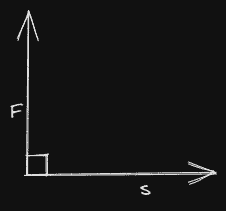

Answer
(d)
$W=Fs\cos\theta$
In the case of option d $\theta=0^0$
therefore work done is maximum
Question 13 A man raises a box of mass 50 Kg to a height of 3 m in 2 minutes, while another man raises the same box to the same height in 4 minutes. What is the ratio of work done by them?
a. 1:1
b. 2:1
c. 1:2
d. 4:1
Answer
(a)
Work done, $W=Fs\cos\theta$
where $F$ is the force applied, $s$ is the displacement and $\theta$ is the angle between force and displacement.
This shows that work done is independent of time.
According to our question, both forces are applied and the direction of movement of the box is the same. So we have $\theta = 0^0$
Both men are raising mass 50 kg to a height of 3 m.
Work done by first man $= mgh$
$=50\times 10\times 3$
$= 1500 J$
Work done by second man $= mgh$
$=50\times 10\times 3$
$= 1500 J$
Hence work done is in the ratio of $1500:1500=1:1$
Question 14 A bullet of mass 10 g leaves a rifle at an initial velocity
of 1000 m/s and strikes the earth at the same level with a velocity of 500 m/s. The work done in joule for overcoming the resistance of the air will be
(a) 375
(b) 3750
(c) 5000
(d) 500
Answer
(b)
Work done = change in kinetic energy
Therefore,
$W=\frac{1}{2}\times 0.01[(1000)^2-(500)^2]=3750J$
Question 15 A body moves a distance of 10 m along a straight line under the action of a 5 N force. If the work done is 25 J, then the angle between the force and direction of motion of the body is
(a) 60°
(b) 75°
(c) 30°
(d) 45°
Answer
(a)
Distance $s=10m$ ; Force $F=5N$ ; and work done $W=25 J$
Work done is given by relation $W=Fs\cos\theta$
Therefore,
$25=5\times 10\cos\theta = 20\cos \theta$
or,
$\cos\theta=\frac{25}{50}=0.5$
or, $\theta=60^0$
Question 16 When a body moves with a constant speed along a circle
(a) no work is done on it
(b) no acceleration is produced in it
(c) its velocity remains constant
(d) no force acts on it.
Answer
(a)
When speed is constant in a circular motion, it means the work done by the centripetal force is zero.