This article’s discussion will center on what lambda in physics means in relation to an electric field. The linear charge density is frequently represented by the symbol \( \lambda \) in the context of electric fields in physics. It is a measurement of the amount of electric charge per unit length along a line, such as a wire or a rod. The linear charge density is measured in Coulombs per meter or C/m.
What is lambda in physics electric field?
The concept of linear charge density, denoted by \( \lambda \), is pivotal in electrostatics for understanding how the electric charge is distributed along one-dimensional objects like wires or rods. By defining \( \lambda \), we can accurately calculate the electric field and electric potential generated by such charged objects, which is essential for understanding electrostatic interactions.
Definitions
- Electric Field (\( \vec{E} \)): A vector field that represents the force experienced by a positive test charge placed at any point in space.
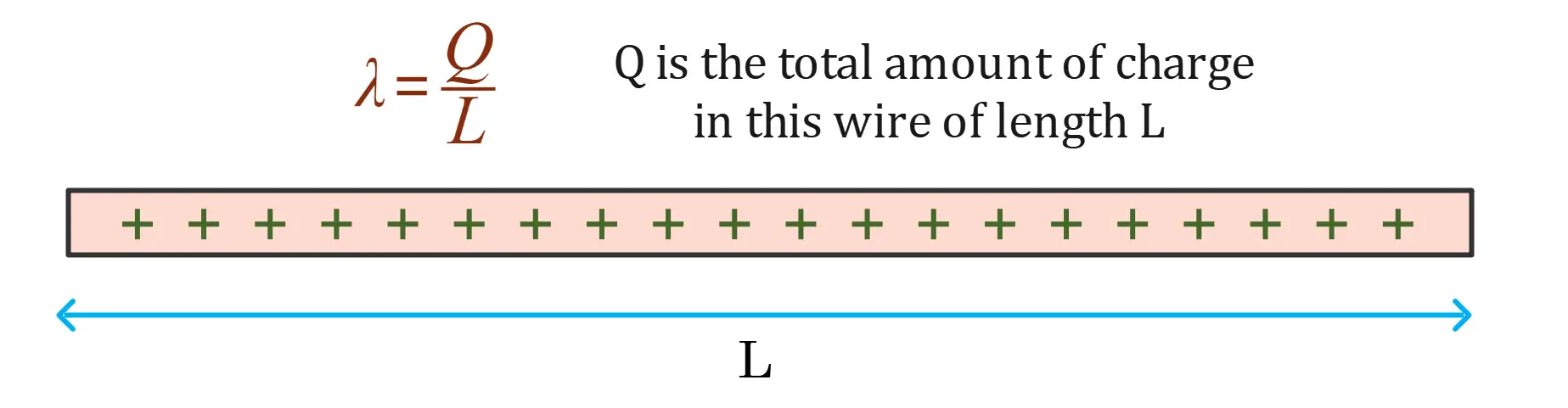
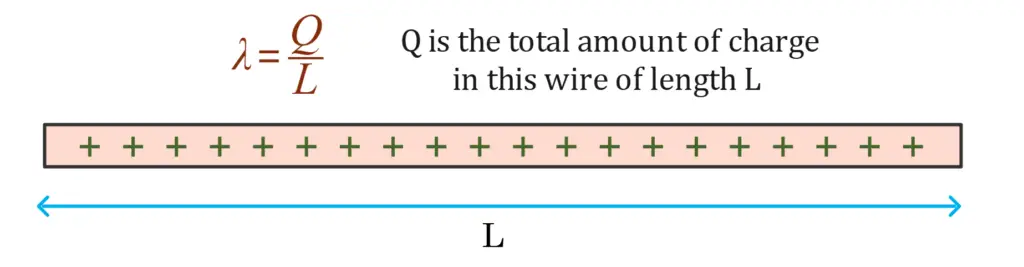
- Linear Charge Density (\( \lambda \)): The amount of charge (\( Q \)) per unit length (\( L \)) along a linear conductor. Mathematically, it is defined as:\[
\lambda = \frac{Q}{L}
\]
Relationship Between \( \lambda \) and Electric Field
The electric field due to a line of charge with linear charge density \( \lambda \) can be calculated using Gauss’s Law or by direct integration, depending on the geometry of the problem. For an infinitely long line of charge, the electric field at a radial distance \( r \) from the line is given by:
\[
\vec{E} = \frac{\lambda}{2\pi \epsilon_0 r} \hat{r}
\]
Here, \( \epsilon_0 \) is the vacuum permittivity, and \( \hat{r} \) is the radial unit vector pointing away from the line of charge.
Questions and Answers
What is the unit of \( \lambda \)?
The unit of \( \lambda \) is Coulombs per meter (C/m).
How does \( \lambda \) affect the electric field?
A higher value of \( \lambda \) would result in a stronger electric field at a given distance from the line of charge.
Can \( \lambda \) be negative?
Yes, \( \lambda \) can be negative, indicating that the line of charge is negatively charged.
How is \( \lambda \) different from surface charge density (\( \sigma \)) and volume charge density (\( \rho \))?
- Linear Charge Density (\( \lambda \)): This is the charge per unit length along a one-dimensional object like a wire or a rod. It is expressed in Coulombs per meter (C/m). Mathematically, it is defined as:\[
\lambda = \frac{Q}{L}
\] - Surface Charge Density (\( \sigma \)): This is the charge per unit area on a two-dimensional surface like a plate. It is expressed in Coulombs per square meter (C/m\(^2\)). Mathematically, it is defined as:\[
\sigma = \frac{Q}{A}
\] - Volume Charge Density (\( \rho \)): This is the charge per unit volume in a three-dimensional object like a sphere. It is expressed in Coulombs per cubic meter (C/m\(^3\)). Mathematically, it is defined as:\[
\rho = \frac{Q}{V}
\]
The primary difference lies in the dimensionality of the object being considered. \( \lambda \) is for one-dimensional objects, \( \sigma \) is for two-dimensional objects, and \( \rho \) is for three-dimensional objects.
Is \( \lambda \) constant for a non-uniformly charged rod?
In the case of a non-uniformly charged rod, \( \lambda \) is not constant along its length. Instead, \( \lambda \) becomes a function of position, \( \lambda(x) \), where \( x \) is the distance along the length of the rod.
This means that the linear charge density can vary from point to point. For such cases, the electric field at a point due to the rod would require integration, taking into account the variable \( \lambda(x) \).
How is \( \lambda \) related to electric potential?
The electric potential \( V \) at a point due to a line of charge can be derived from the electric field \( \vec{E} \). For an infinitely long line of charge with a constant \( \lambda \), the electric potential \( V \) at a radial distance \( r \) from the line is given by:
\[
V = – \int \vec{E} \cdot d\vec{r} = – \int \frac{\lambda}{2\pi \epsilon_0 r} dr
\]
Upon integration, you’ll find that the electric potential varies logarithmically with distance \( r \) and is directly proportional to \( \lambda \).
\[
V = – \frac{\lambda}{2\pi \epsilon_0} \ln(r) + C
\]
Here, \( C \) is the constant of integration, which can be determined based on boundary conditions.