We already know what is speed in physics. In this article, we will learn about instantaneous speed. We would also look at a few example questions based on instantaneous speed.
Speed Definition
Speed is defined as the rate at which the position of any object changes over time. An object’s speed might vary as it moves.
Instantaneous Speed
Definition
Instantaneous speed is the speed of a moving object at any particular instant of time.
It is a term used to describe the speed of an object at any one point in time. The instantaneous speed of a moving object might vary from one moment to another.
A moving car’s speedometer, for example, displays the instantaneous speed at which the car is moving. At one instant of time, the car’s instantaneous speed maybe 60 mph, and in the very next moment, applying a tiny push force on the accelerator pedal may cause the instantaneous speed to increase to 66 mph.
Instantaneous Speed Formula
An object’s instantaneous speed can also be described as a short distance travelled divided by the time it takes to cover that distance.
The instantaneous speed formula is given by the relation
$$\text{Instantaneous Speed, }v_i=\lim_{\Delta t\rightarrow 0}\frac{s(t+\Delta t)-s(t)}{\Delta t}$$
or,
$$v_i=\lim_{\Delta t\rightarrow 0}\frac{\Delta s}{\Delta t}=\frac{ds}{dt}$$
where,
$v_i$ is the instantaneous speed
$\Delta s$ is change in value of $s$
$\Delta t$ is change in time $t$
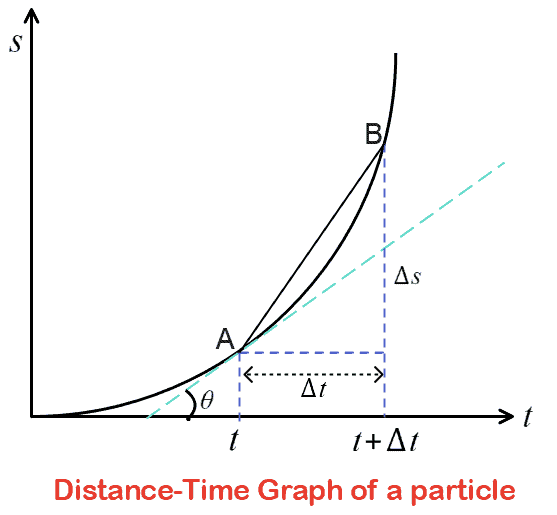
The figure given below shows a distance-time graph. The slope of the tangent to the graph at time $t$ gives the speed at time $t$. The slope of chord $AB$, as shown in the distance-time graph below, gives the average speed between $t$ and $t+\Delta t$. $A$ and $B$ are the points on the curve corresponding to time $t$ and $t+\Delta t$, respectively.
If $\Delta t \rightarrow 0$, the chord $AB$ becomes the tangent to the curve at the point $A$, and the average speed $\frac{\Delta s}{\Delta t}$ becomes the slope of the tangent and is expressed as $\frac{ds}{dt}$.
Here, $ds$ is the small distance covered and $dt$ is the small time taken in travelling the same distance.
Important Points To Remember
- The instantaneous speed is never less than or equal to zero.
- It is a scalar quantity.
- The instantaneous speed of uniform motion is constant.
- The magnitude of instantaneous velocity at any given time is the magnitude of instantaneous speed at that time.
- It is a limit taken over the average speed when the time interval becomes very small or approaches zero.
How to Calculate Instantaneous Speed
Now we know about the instantaneous speed definition and formula, let us now look at some example problems on how to calculate it.
Example Question:- When an object is dropped from a particular height, it begins to fall under the influence of gravity. The object’s position changes in accordance with the function $s(t)=10t^2$, where $s(t)$ is measured in meters. Calculate the object’s instantaneous speed at $t=15$ seconds.
Solution:-
We know that instantaneous speed is given by the relation
$v_i=\lim_{\Delta t\rightarrow 0}\frac{\Delta s}{\Delta t}=\frac{ds}{dt}$
It is given in the question that
$s(t)=10t^2$,
We can find instantaneous velocity by differentiating $s(t)$ with respect to time.
$\Rightarrow v_i=(\frac{ds}{dt}){t=15}$
Now,
$\frac{ds}{dt}=\frac{d}{dt}(10t^2)=2\times 10 \times t$
So,
$\Rightarrow v_i=(\frac{ds}{dt}){t=15}=2\times 10 \times 15 = 300 m/s$
The instantaneous speed at $t=10 s$ is $300 m/s$