While studying physics, we often encounter situations where we need to define the position of a point in space. This is where the concept of coordinates comes into play. Let’s take a closer look at what we mean by coordinates and explore their role in our study of physics.
Coordinates in Physics
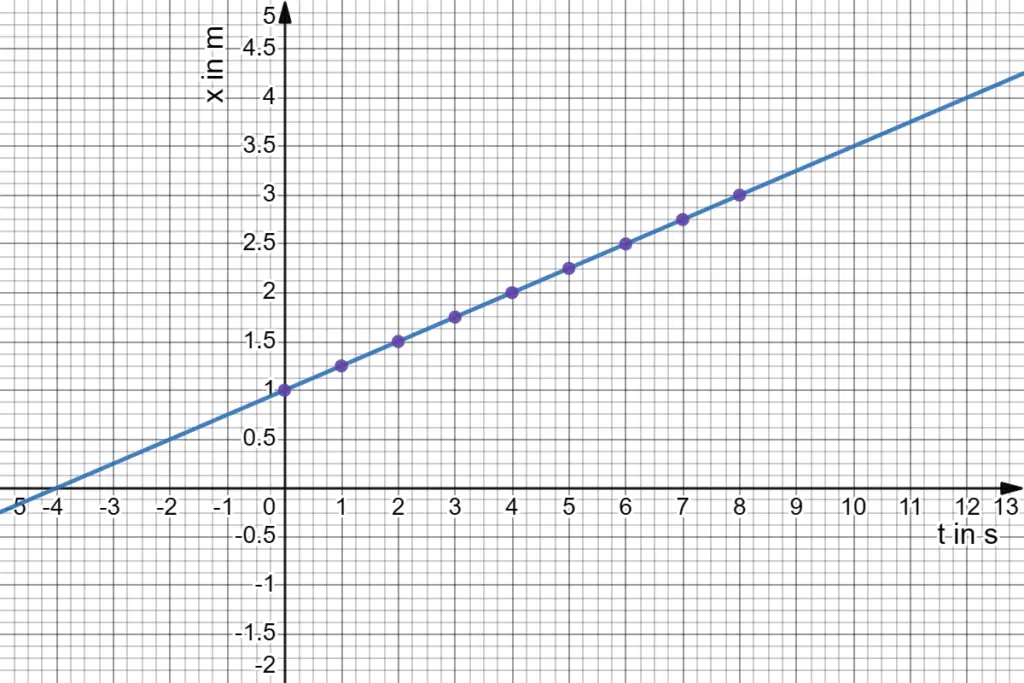
In the simplest terms, coordinates are numerical values that define the position of a point or an object within a space relative to a fixed reference, often called the origin. The coordinates of a point are the distances from the point to a set of reference lines or planes, also known as axes.
What is a Coordinate System?
A coordinate system, in physics, can be defined as a mathematical framework that allows us to specify the position of a point in space with reference to a set of axes or planes. It essentially provides a basis for measuring distances and angles and can be used to describe the location of objects in a given space.
A coordinate system can be seen as a particular frame of reference in which an observer can measure properties such as position, velocity, and acceleration of a physical object. In other words, a coordinate system serves as a frame of reference that allows us to describe the physical location and motion of objects in a standardized and quantifiable manner.
It’s important to note that the choice of a coordinate system or frame of reference can greatly simplify the mathematical expressions of physical laws, and different systems can be used depending on the specific problem at hand.
Cartesian Coordinate System
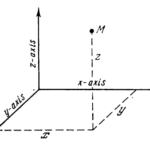
The Cartesian coordinate system was named after René Descartes. This is the most common coordinate system used in physics. It uses two or three perpendicular axes to define a point in space. In a two-dimensional space, a point is defined by (x, y), and in a three-dimensional space, a point is defined by (x, y, z). The coordinates x, y, and z are the distances from the point to the x, y, and z axes, respectively.
It’s used in mechanics to describe the position and motion of objects in space. It’s also used in electromagnetism to describe electric and magnetic fields, and in quantum mechanics to describe the state of particles.
Polar Coordinate System
The polar coordinate system is another commonly used system in physics. It defines a point in a plane using a distance and an angle. The coordinates are usually denoted as (r, θ), where r is the distance from the origin and θ is the angle from the reference direction. The relationship between Cartesian and polar coordinates is given by:
\(x = r \cos \theta\)
\(y = r \sin \theta\)
This system is particularly useful in situations that involve circular, cylindrical, or spherical symmetry, such as the motion of planets in their orbits, or the propagation of waves from a point source. It’s also used in navigation and in the study of fluid dynamics.
Spherical Coordinate System
The spherical coordinate system is used to define a point in three-dimensional space. It uses two angles and a distance from a reference point. The coordinates are usually denoted as (r, θ, φ). The relationship between Cartesian and spherical coordinates is given by:
\(x = r \sin \phi \cos \theta\)
\(y = r \sin \phi \sin \theta\)
\(z = r \cos \phi\)
This system is used when dealing with phenomena that exhibit spherical symmetry, such as the propagation of electromagnetic waves from a point source, or the gravitational field around a point mass. It’s also used in quantum mechanics to solve the Schrödinger equation for atoms.
Cylindrical Coordinate System
The cylindrical coordinate system is a type of coordinate system that uses a distance, an angle, and a height to define a point in three-dimensional space. The coordinates are usually denoted as (ρ, φ, z), where ρ is the radial distance from the z-axis, φ is the azimuthal angle, and z is the height along the z-axis. The relationship between Cartesian and cylindrical coordinates is given by:
\(x = \rho \cos \phi\)
\(y = \rho \sin \phi\)
\(z = z\)
This system is used in situations that involve cylindrical symmetry, such as the flow of fluid around a cylinder, the magnetic field around a wire, or the vibrations of a circular membrane. It’s also used in electrical engineering to solve problems involving cylindrical capacitors or coaxial cables.
Questions for Review
- How are points defined in a Cartesian coordinate system?
- What is the relationship between Cartesian and polar coordinates?
- How are points defined in a spherical coordinate system?
- What is the relationship between Cartesian and cylindrical coordinates?
Answer
- In a Cartesian coordinate system, points are defined by the distances from the point to the x, y, and z axes.
- The relationship between Cartesian and polar coordinates is given by \(x = r \cos \theta\) and \(y = r \sin \theta\).
- In a spherical coordinate system, points are defined by two angles and a distance from a reference point.
- The relationship between Cartesian and cylindrical coordinates is given by \(x = \rho \cos \phi\), \(y = \rho \sin \phi\), and \(z = z\).