Velocity is a vector quantity that describes the rate of change of an object’s position with respect to time. It is often denoted by the symbol \( \vec{v} \) and has both magnitude and direction. In this discussion, we will explore the concept of the derivative of velocity, which leads us to the concept of acceleration.
Definitions
Velocity
Velocity is defined as the rate of change of displacement (\( \vec{s} \)) with respect to time (\( t \)). Mathematically, it is expressed as:
\[
\vec{v} = \frac{{d\vec{s}}}{{dt}}
\]
Derivative
The derivative of a function represents the rate at which the function changes as its input changes. In the context of velocity, the derivative gives us the rate of change of velocity, which is acceleration.
For more information consider reading these articles
The derivative of Velocity is Acceleration
Mathematical Representation
The derivative of velocity with respect to time gives us acceleration. Mathematically, this is expressed as:
\[
\vec{a} = \frac{{d\vec{v}}}{{dt}}
\]
Here, \( \vec{a} \) is the acceleration vector, \( \vec{v} \) is the velocity vector, and \( t \) is time. The derivative operation \( \frac{{d}}{{dt}} \) indicates that we are finding the rate of change of velocity with respect to time.
Acceleration describes how quickly an object is speeding up or slowing down. It has units of \( \text{m/s}^2 \) in the International System of Units (SI).
Components of Acceleration
In a Cartesian coordinate system, the acceleration vector \( \vec{a} \) can be broken down into its components \( a_x \), \( a_y \), and \( a_z \) along the \( x \), \( y \), and \( z \) axes, respectively. If the velocity vector \( \vec{v} \) has components \( v_x \), \( v_y \), and \( v_z \), then:
\[
a_x = \frac{{dv_x}}{{dt}}, \quad a_y = \frac{{dv_y}}{{dt}}, \quad a_z = \frac{{dv_z}}{{dt}}
\]
Types of Acceleration
1. Constant Acceleration
In cases where acceleration is constant, the velocity function \( \vec{v}(t) \) will be a linear function of time \( t \). The relationship between velocity and time can be expressed as:
\[
\vec{v}(t) = \vec{v}_0 + \vec{a} \cdot t
\]
Here, \( \vec{v}_0 \) is the initial velocity and \( \vec{a} \) is the constant acceleration.
2. Variable Acceleration
When acceleration is not constant, it can be a function of time \( t \), velocity \( \vec{v} \), or even position \( \vec{s} \). In such cases, the relationship between velocity and acceleration becomes more complex and may require integration or differential equations to solve.
\[
\vec{a}(t) = \frac{{d\vec{v}(t)}}{{dt}}
\]
Direction and magnitude of Acceleration
1. Direction: The direction of the acceleration vector indicates the direction in which the velocity is changing.
2. Magnitude: The magnitude of the acceleration vector tells us how quickly the velocity is changing.
Interpretation of derivative of velocity
1. Constant Acceleration: If the acceleration is constant, the velocity function will be a linear function of time.
2. Zero Acceleration: If the acceleration is zero, the velocity remains constant.
3. Negative Acceleration: Also known as deceleration, it indicates that the object is slowing down.
Questions and Answers
What is the unit of acceleration?
The unit of acceleration is \( \text{m/s}^2 \).
How is instantaneous acceleration calculated?
Instantaneous acceleration is calculated as the limit of the average acceleration over an infinitesimally small time interval \( \Delta t \) as it approaches zero.
\[
\vec{a} = \lim_{{\Delta t \to 0}} \frac{{\Delta \vec{v}}}{{\Delta t}}
\]
Can acceleration be negative?
Yes, negative acceleration, often termed as deceleration, indicates that the object is slowing down.
How is acceleration different from velocity?
While velocity describes the rate of change of position, acceleration describes the rate of change of velocity. Both are vector quantities, meaning they have both magnitude and direction.
What happens when acceleration is zero?
When acceleration is zero, it implies that the velocity of the object remains constant; the object moves with a steady speed in a fixed direction.
By understanding the derivative of velocity in terms of acceleration, you can better comprehend the dynamics of motion, which is a cornerstone in the field of physics. This knowledge is particularly useful for solving problems related to kinematics and dynamics.
What is the relationship between displacement, velocity, and acceleration?
Displacement (\( \vec{s} \)), velocity (\( \vec{v} \)), and acceleration (\( \vec{a} \)) are related through derivatives. The first derivative of displacement with respect to time is velocity, and the first derivative of velocity with respect to time is acceleration.
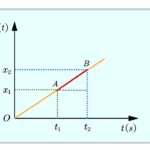
How do you find acceleration from a velocity-time graph?
The slope of a velocity-time graph at any point gives the instantaneous acceleration at that point.
What is the second derivative of displacement?
The second derivative of displacement with respect to time is acceleration:
\[
\frac{{d^2\vec{s}}}{{dt^2}} = \vec{a}
\]
By understanding the derivative of velocity, you gain a deeper insight into the concept of acceleration, which is fundamental to the study of motion in physics.