Acceleration and distance are related through the equations of motion, specifically through the displacement equation. The relationship is not linear but quadratic, meaning that the distance traveled by an object with constant acceleration is proportional to the square of the time elapsed.
How does acceleration relate to distance?
The key equation that relates acceleration to distance is:
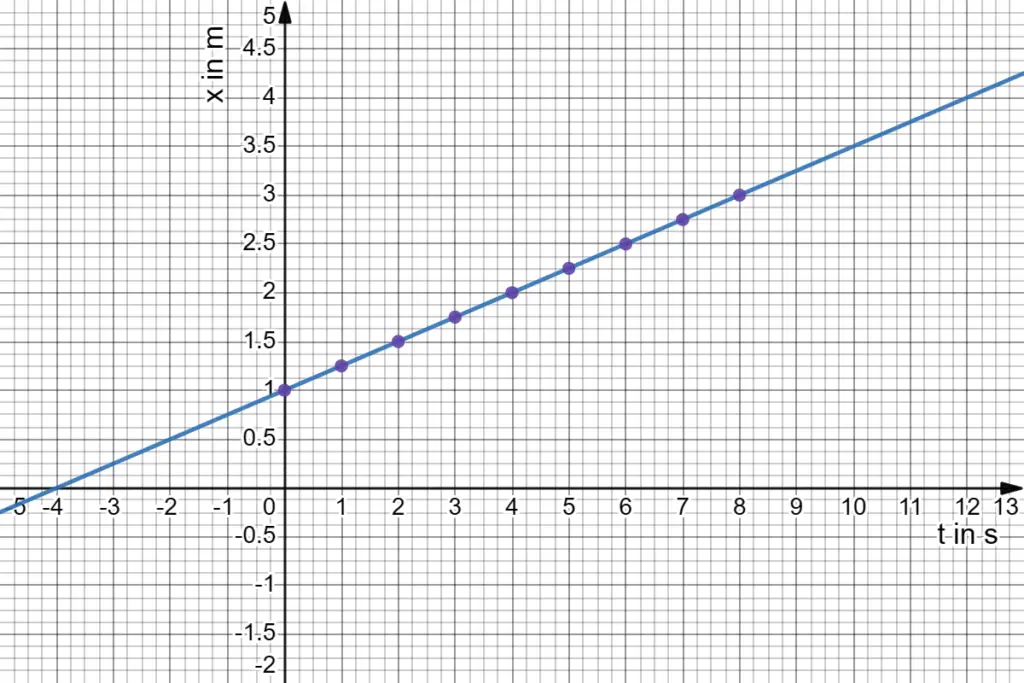
$s = ut + \frac{1}{2}at^2$
Where:
- $s$ is the displacement (distance traveled)
- $u$ is the initial velocity
- $a$ is the acceleration
- $t$ is the time elapsed
This equation shows that the distance traveled by an object under constant acceleration is the sum of two components:
- The distance it would have traveled at constant velocity ($ut$)
- An additional distance due to acceleration ($\frac{1}{2}at^2$)
To understand this relationship better, let’s break it down:
- Constant velocity component: If there were no acceleration, the object would travel a distance of $ut$ in time $t$. This is simply the product of velocity and time.
- Acceleration component: The $\frac{1}{2}at^2$ term represents the additional distance traveled due to acceleration. This term is quadratic in time, meaning that as time increases, this component grows much faster than the constant velocity component.
The quadratic nature of this relationship means that small changes in acceleration can lead to large changes in distance traveled over time. For example, doubling the acceleration will quadruple the distance traveled in a given time period, assuming the initial velocity remains the same.
It’s important to note that this equation assumes constant acceleration. In real-world scenarios, acceleration may vary, which would require more complex calculations or calculus to determine the exact relationship between acceleration and distance.
Another way to relate acceleration to distance is through the equation:
$v^2 = u^2 + 2as$
This equation allows us to calculate the final velocity ($v$) of an object that has accelerated over a certain distance ($s$), without needing to know the time taken. It shows that the change in the square of velocity is proportional to both the acceleration and the distance traveled.
In practical applications, understanding this relationship is crucial in fields such as automotive engineering (for calculating braking distances), aerospace (for determining launch trajectories), and physics education. It forms the foundation for more complex motion analysis and is a key concept in classical mechanics.
Mind Map on Relation between distance and acceleration