In physics, it is often necessary to convert between coordinate systems, such as switching from cartesian to spherical coordinates, especially when dealing with problems that involve symmetry or complex three-dimensional shapes.
In this article learn about converting from a cartesian to spherical coordinate system.
Cartesian to Spherical Coordinate Conversion
Cartesian Coordinates
Cartesian coordinates use three variables, usually denoted as \( x, y, \) and \( z \), to describe a point in three-dimensional space.
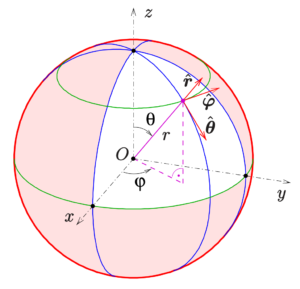
Spherical Coordinates
Spherical coordinates, on the other hand, use three variables: \( r, \theta, \) and \( \phi \), where:
- \( r \) is the distance from the origin to the point.
- \( \theta \) is the angle between the positive x-axis and the projection of the radius vector onto the xy-plane.
- \( \phi \) is the angle between the positive z-axis and the radius vector.
Conversion from Cartesian to Spherical Coordinate
The conversion between these two coordinate systems involves trigonometric functions and can be described as follows:
1. Calculate the Radial Distance \( r \): It is the distance from the origin to the point. It can be found using the Pythagorean theorem:
\[
r = \sqrt{x^2 + y^2 + z^2}
\]
2. Calculate the Polar Angle \( \theta \): It is measured from the positive x-axis. The tangent of this angle is the ratio of \( y \) to \( x \), and it can be found using the arctangent function:
\[
\theta = \arctan\left(\frac{y}{x}\right)
\]
3. Calculate the Azimuthal Angle \( \phi \): It is measured from the positive z-axis. The cosine of this angle is the ratio of \( z \) to \( r \), and it can be found using the arccosine function:
\[
\phi = \arccos\left(\frac{z}{r}\right)
\]
Example
Let’s consider a point with Cartesian coordinates \( (x, y, z) = (1, 1, 1) \). How can we find the spherical coordinates of this point?
– Calculating \( r \):
\[
r = \sqrt{1^2 + 1^2 + 1^2} = \sqrt{3}
\]
– Calculating \( \theta \):
\[
\theta = \arctan\left(\frac{1}{1}\right) = 45^{\circ}
\]
– Calculating \( \phi \):
\[
\phi = \arccos\left(\frac{1}{\sqrt{3}}\right) \approx 54.74^{\circ}
\]
So the spherical coordinates are \( (r, \theta, \phi) = \left(\sqrt{3}, 45^{\circ}, 54.74^{\circ}\right) \).
Summary
Given below are the steps to convert from Cartesian coordinates to Spherical coordinates:
1. Radial Distance \( r \):
\[ r = \sqrt{x^2 + y^2 + z^2} \]
2. Polar Angle \( \theta \):
\[ \theta = \arctan\left(\frac{y}{x}\right) \]
3. Azimuthal Angle \( \phi \):
\[ \phi = \arccos\left(\frac{z}{r}\right) \]
Remember that \( r \) gives the distance from the origin to the point, \( \theta \) is the angle in the xy-plane from the positive x-axis, and \( \phi \) is the angle from the positive z-axis to the point.