Uniform Acceleration

Uniform acceleration is a specific type of motion in which an object’s velocity changes at a constant rate over time. It serves as a foundational concept in physics, particularly in the study of mechanics. The purpose of this article is to give readers a thorough understanding of uniform acceleration by looking into its definition, characteristics, kinematic equations, graphical representations, and real-world examples.

Definition of Uniform Acceleration

If the velocity of a body changes by an equal amount in an equal interval of time, however, small the interval may be then its acceleration is said to be uniform.

Uniform acceleration ($ a $) can also be defined as the rate of change of velocity per unit time, where this rate of change remains constant. In mathematical terms, uniform acceleration is defined by the equation:

\[
a = \frac{{\Delta v}}{{\Delta t}}
\]

Here, $ \Delta v $ represents the change in velocity, and $ \Delta t $ denotes the change in time.

Characteristics of Uniform Acceleration

Understanding the nuances of uniform acceleration becomes easier when we delve into its core characteristics. Here is a detailed breakdown:

Constant Rate of Change in Velocity

In uniform acceleration, the velocity of an object changes at a consistent rate.

Applicability of Kinematic Equations

Uniformly accelerated motion can be described using three fundamental kinematic equations:
1. $ v = u + at $
2. $ s = ut + \frac{1}{2}at^2 $
3. $ v^2 = u^2 + 2as $

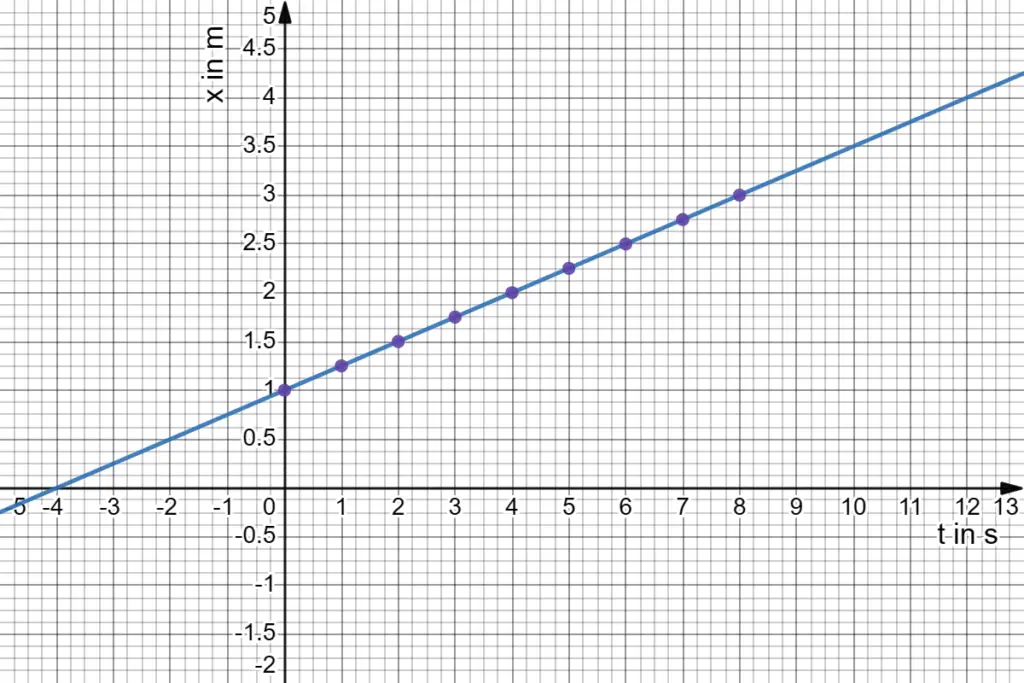
Linear Velocity-Time Graph

A velocity-time graph for uniform acceleration is a straight line, and its slope equals the value of the constant acceleration.

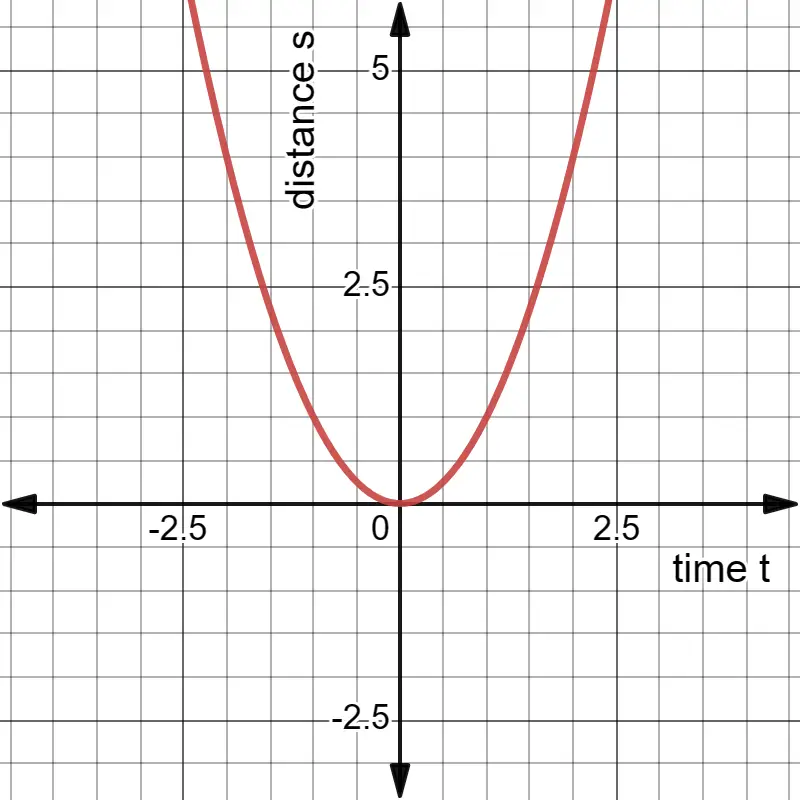
Parabolic Displacement-Time Graph

The displacement-time graph for such motion is a parabola, arising from the quadratic relationship $(\frac{1}{2}at^2)$ between displacement and time in the second equation of motion.

The figure given below shows the distance-time graph of an object moving with a uniform accelerated motion where acceleration $a=2m/s^2$.

Importance of Initial Conditions

Initial velocity ($ u $) and initial position ($ s_0 $) are essential parameters for problem-solving in uniformly accelerated motion. These conditions act as the starting point for any calculations involving kinematic equations.

Idealized Conditions

It is often an idealized model but serves as a practical approximation for real-world applications like free-falling objects in a vacuum or a car accelerating on a straight road.

Directional Aspects

Both the velocity and acceleration vectors can be in the same or opposite directions, determining whether the object speeds up or slows down.

Kinematic Equations for Uniformly Accelerated Motion

Uniformly accelerated motion can be modeled using the following kinematic equations:

1. First Equation of Motion
\[
v = u + at
\]

2. Second Equation of Motion:
\[
s = ut + \frac{1}{2} a t^2
\]

3. Third Equation of Motion:
\[
v^2 = u^2 + 2as
\]

These equations allow us to relate position, velocity, and acceleration to time, making them invaluable tools for problem-solving.

Graphical Interpretation

In uniformly accelerated motion, different graphs can portray the relationship between parameters:

Velocity-Time Graph: A straight line indicates uniform acceleration, and its slope is equal to the value of the constant acceleration.
Displacement-Time Graph: This graph is a parabola, highlighting the quadratic nature of the relationship between displacement and time.

Examples of Uniform Acceleration

Understanding uniform acceleration conceptually often benefits from specific examples. Below are points illustrating scenarios where uniform acceleration is observed or can be a reasonable approximation.

Falling Objects in a Vacuum

Context: An object falling freely near the Earth’s surface in the absence of air resistance.
Acceleration: The gravitational acceleration $ g = 9.81 \, \text{m/s}^2 $ is constant.
Example Calculation: If an object starts from rest, its velocity after 2 seconds would be $ v = gt = 9.81 \times 2 = 19.62 \, \text{m/s} $.

Cars Accelerating from Rest

Context: A car accelerates from rest to reach a certain speed on a straight road.
Acceleration: Constant force from the engine results in constant acceleration.
Example Calculation: With $ a = 2 \, \text{m/s}^2 $ and starting from rest ($ u = 0 $), the car’s velocity after 3 seconds would be $ v = at = 2 \times 3 = 6 \, \text{m/s} $.

Inclined Plane without Friction

Context: An object sliding down an inclined plane without friction.
Acceleration: The component of the gravitational force along the incline provides a constant acceleration.
Example Calculation: If the incline is at $ 30^\circ $ and neglecting friction, the acceleration $ a = g \sin(30^\circ) = 4.905 \, \text{m/s}^2 $.

Spacecraft Thrust

Context: A spacecraft in outer space applying constant thrust.
Acceleration: Due to the constant thrust and lack of air resistance in space, the acceleration remains constant.
Example Calculation: With $ a = 0.5 \, \text{m/s}^2 $, the spacecraft’s velocity after 10 seconds from rest would be $ v = at = 0.5 \times 10 = 5 \, \text{m/s} $.

Elevator Moving Upward

Context: An elevator starts from rest and moves upward with constant acceleration.
Acceleration: The motor provides a constant force, and thus, the acceleration is constant.
Example Calculation: If $ a = 1 \, \text{m/s}^2 $, the elevator’s velocity after 4 seconds from rest would be $ v = at = 1 \times 4 = 4 \, \text{m/s} $.

Each of these examples can be analyzed using the kinematic equations for uniformly accelerated motion. They serve as practical applications of the concept, aiding in your understanding and problem-solving skills.

Questions and Answers

Is gravitational acceleration a form of uniform acceleration?

Yes, in a vacuum, gravitational acceleration is approximately constant near the Earth’s surface.

How can time $ t $ be calculated using the first equation of motion

Time can be determined by rearranging the first equation: $ t = \frac{v-u}{a} $.

Is uniform acceleration applicable in circular motion?

No, because the direction of acceleration changes continuously in circular motion.

By understanding its definitions, characteristics, and associated equations, you lay the groundwork for solving a wide range of problems in physics. Whether you’re observing a car accelerating on a straight road or an object free-falling in a vacuum, the concept of uniform acceleration frequently applies, making it essential for any student or practitioner of physics.