In this article, we will learn how to find displacement on a position-time graph. A position-time graph is a graph where the instantaneous position \(x\) of a particle is plotted on the y-axis and the time \(t\) on the x-axis. The position-time graph shows you where an object is located over a certain interval of time or at any particular instant of time.
Key takeaways:
- Displacement can be found on a position-time graph by drawing a line to get the projection of a point on the y-axis, which gives the position of the object at that point.
- The displacement between two points on the position-time graph can be calculated by subtracting the initial position from the final position. Negative displacement means distance in the negative direction.
Displacement of any object is defined as the change in position of the object in a fixed direction. It is given by the vector drawn from the initial position to the final position of the object.
Displacement is a vector quantity i.e., it has both magnitude and direction. The displacement of an object can be positive, negative, and zero.
How to find displacement on a position-time graph
To learn how you can find displacement on a position-time graph consider the figure given below that shows a position-time graph of any object.
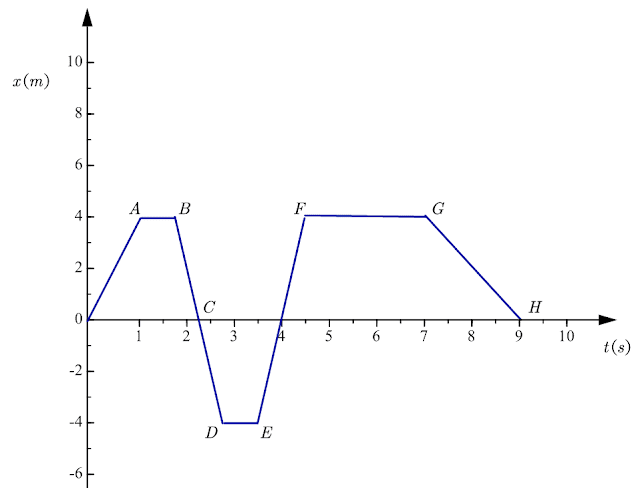
Now from the above figure, we can see that our object under consideration starts its journey from the origin at initial time \(t=0\) and position \(x=0\). It reaches its final position at the time \(t=9s\) represented by point \(H\) on the position-time graph.
Let us now find the displacement of the object when it reaches point \(A\) marked on the graph. Let us now draw a line to get a projection of point \(A\) on the y-axis to get the position of the object when it reaches point \(A\). The figure given below shows the projection of various points on both the x-axis and the y-axis.
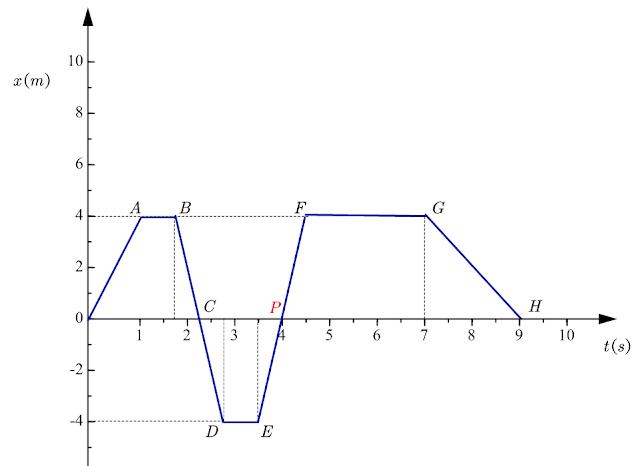
The projection of a point \(A\) on the y-axis is at point \(4m\) from the origin. So,
Position of the object with respect to the origin when it reached point \(A\) \(= 4m\)
Position of the object with respect to the origin when it reaches point \(B\) \(= 4m\)
From the position-time graph, we can see that the projection of \(B\) on the y-axis is at position \(x=4m\) which means the object is at rest and has not moved with the passage of time.
Similarly, you can find the position of the object at various points with respect to the origin \(O\) or initial position of the object.
Let us now find the displacement of the object between time \(t=0\,\,s\) to \(t=3.5\,\,s\).
At \(t=4s\) our object is at point \(P\).
We know that displacement is a change in the position of the object.
Here,
\(x_0=0m\)
\(x_{3.5}=-4m\)
So, change in position = displacement =\(x_{3.5} – x_0\,\,=\,\,-4-0=-4m\)
Note that here displacement is negative. Negative displacement means distance in the negative direction. So, instead of 4 m forward from the origin, the object is 4 m backward from the origin.
Let us now find the displacement of the object between time \(t=0\,\,s\) to \(t=4\,\,s\).
At \(t=4s\) our object is at point \(P\).
Here
\(x_0=0m\)
\(x_4=0m\)
So, change in position = displacement =\(x_4 – x_0\,\,=\,\,0m\)
Similarly, you can find displacement between any time interval using the position-time graph.



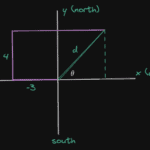
The displacement of B relative to origin is not 4 m but rather the (straightline) distance (use Pythagoras) from origin to B.
You are right the displacement of B relative to origin is not 4m. But if you read carefully then we are talking about Position of the object with respect to the origin when it reaches point B which is equal to 4m. Here we are trying to find displacement between any given time interval using the position-time graph
Good information