We will learn about instantaneous velocity in depth in this article. We already understand what average velocity is. The average velocity provides an overall understanding of the object’s motion. It provides no information about the velocity of the object at any given point in time.
Instantaneous velocity
Key Takeaways
- Instantaneous velocity is different from average velocity.
- To find instantaneous velocity, we use the formula: $$v=\lim_{\Delta t\rightarrow 0}\frac{\Delta x}{\Delta t}$$
- Instantaneous velocity is the derivative of the coordinate with respect to time.
- For uniform motion, the instantaneous velocity is constant.
Instantaneous Velocity Example
In physics, knowing the object’s instantaneous velocity is sometimes required. Here are two examples of why we need to define instantaneous velocity and why we need it even if we know the average velocity of the object.
- For example, if we want to learn about the range and shape of a projectile’s path, we need to know its initial velocity, not its average velocity.
- Another example of when we need instantaneous velocity rather than average velocity is when a body collides with an obstacle. When a body collides with an obstacle, the force it exerts on the obstacle is determined by its velocity at the moment of collision rather than its average velocity.
How to determine the instantaneous velocity of a particle
Let us now learn how to find the instantaneous velocity of a particle.
- Let $x$ be the coordinate of a moving object at time $t$.
- At the time $t_1=t+\Delta t$ the coordinates will be $x_1=x+\Delta x$, where $\Delta x$ is the displacement.
- Now average velocity is given by the relation
$$v_{av}=\frac{x_2-x_1}{t_2-t_1}=\frac{x+\Delta x-x}{t+\Delta t-t}=\frac{\Delta x}{\Delta t}$$ - The longer the time interval $\Delta t$, the greater the difference between the average velocity and the instantaneous value.
- On the other hand, the average velocity deviates from the desired instantaneous velocity less when the time period $\Delta t$ is shorter.
- We can now define the instantaneous velocity $v$ as the limiting value that the average velocity approaches for an infinitely small time interval.
$$v=\lim_{\Delta t\rightarrow 0}v_{av}=\lim_{\Delta t\rightarrow 0}\frac{\Delta x}{\Delta t}$$ - Such a limiting value is referred to as a derivative in mathematics. As a result, the instantaneous velocity is the derivative of the coordinate with respect to time.
Instantaneous velocity for uniform motion
Since a particle in uniform motion has a constant average velocity, its limiting value is the constant itself. Thus, the instantaneous velocity of a particle in uniform motion is constant.
So motion with constant velocity can be referred to as uniform motion. This means that the object covers equal distances in equal amounts of time.
Consequently, in the equation of uniform motion, $x=vt+b$, constant $v$ represents the motion’s velocity and constant $b$ represents the initial coordinate.
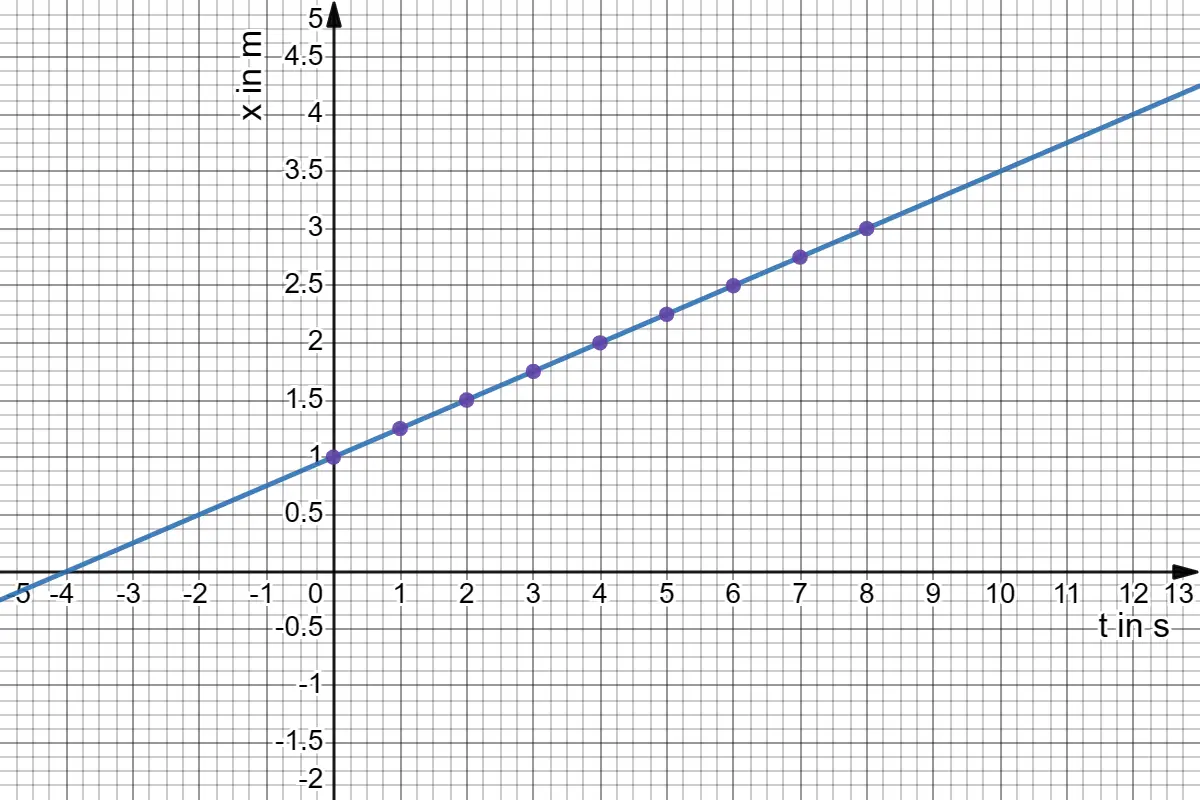
Consider the graph for uniform motion
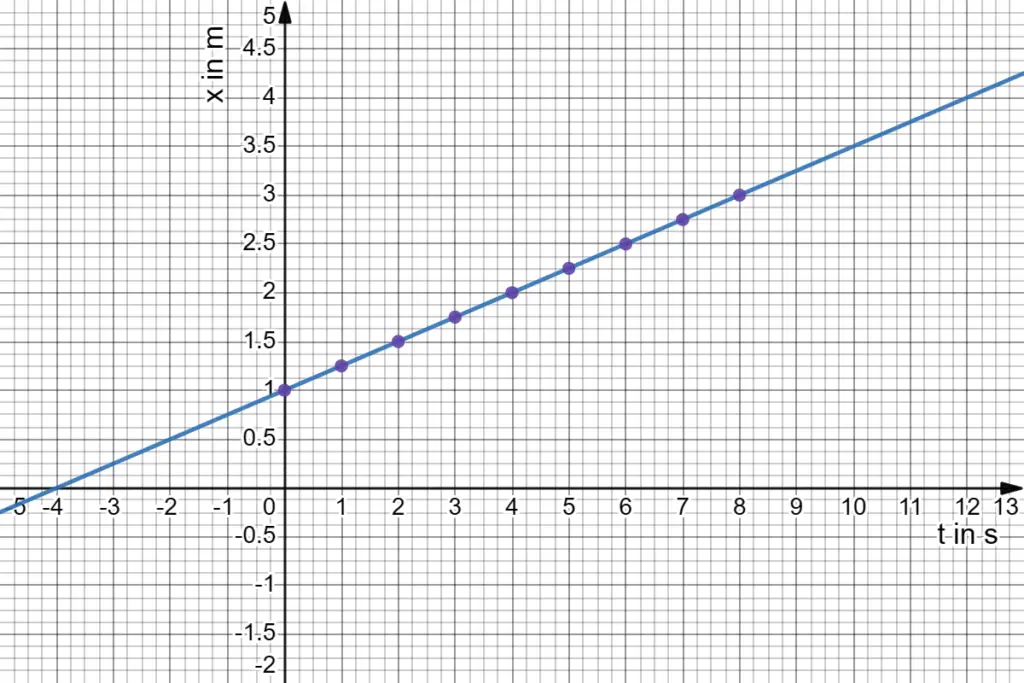
So, when you graph the motion of an object moving at a constant velocity (uniform motion), the velocity of the object can be determined by looking at the angle of the line on the graph.
The steeper the line, the faster the object is moving. The speed of the object is equal to the tangent of the angle that the line makes with the time axis on the graph.
Frequently asked questions
What is instantaneous velocity?
Instantaneous velocity is the speed and direction of an object at a specific point in time. It is different from average velocity, which is the total displacement divided by the total time interval.
How do you calculate instantaneous velocity?
Instantaneous velocity can be calculated by finding the slope of the tangent line to a position-time graph at a given point. Alternatively, it can be calculated by taking the limit of the average velocity as the time interval approaches zero.
What are some examples of instantaneous velocity?
Some examples of instantaneous velocity are:
- The speedometer of a car shows the instantaneous velocity of the car at any moment.
- The velocity of a falling object at a certain height is its instantaneous velocity at that point.
- The velocity of a projectile at the highest point of its trajectory is its instantaneous velocity at that point.
What is the difference between instantaneous velocity and instantaneous speed?
Instantaneous velocity is a vector quantity, which means it has both magnitude and direction. Instantaneous speed is a scalar quantity, which means it only has magnitude. Instantaneous speed is the absolute value of instantaneous velocity.
What are some applications of instantaneous velocity?
Some applications of instantaneous velocity are:
- Measuring the acceleration of an object by finding the rate of change of its instantaneous velocity.
- Determining the direction of motion of an object by finding the angle of its instantaneous velocity vector.
- Analyzing the motion of objects in circular or curved paths by finding their instantaneous velocities at different points.
Summary
In summary, understanding the difference between instantaneous and average velocity is crucial in physics. Instantaneous velocity is vital for projectile motion and collision force calculations. It is found using the limiting value of average velocity as the time interval approaches zero, represented as a derivative. For uniform motion, the instantaneous velocity is constant, and the equation is $x=vt+b$. In a graph of uniform motion, the object’s velocity is determined by the angle of the line, with speed equal to the tangent of the angle with the time axis.