In this article, we will learn how to find instantaneous velocity on a position-time graph.
What is instantaneous velocity?
First of all, let us look at the definition of instantaneous velocity.
The instantaneous velocity of a particle is the velocity of the particle at any instant of time or at any point on its path.
We are interested in the instantaneous velocity of the particle when the particle is moving with variable velocity along its path. It tells us about how fast an object is moving anywhere along its path.
How to find instantaneous velocity on a position-time graph
Before going any further I would like to advise you to read this article on How to find average velocity on a position-time graph.
From this article, we came to know that
The slope of the straight line joining two points on the position-time graph gives the average velocity of the particle between these two points.
Consider the figure given below which shows a position-time graph of a body moving with variable velocity.
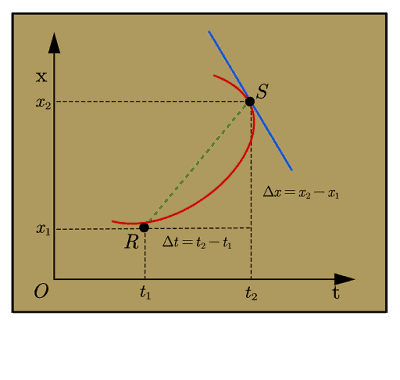
It is clear from this figure that the average velocity of the particle between points \(R\) and \(S\) is given by the relation \[v_{avg}=\text{slope of RS}=\frac{x_2-x_1}{t_2 -t_1}=\frac{\Delta x}{\Delta y}\] We have to find the instantaneous velocity of particle at point \(S\). Please note that the object is moving from point \(R\) towards point \(S\).
Instantaneous velocity is the limiting value of the average velocity \(\frac{\Delta x}{\Delta y}\) as \(\Delta y\) approaches zero. So we have,
\[\vec{v}=\underset{\Delta t\rightarrow 0}{\lim}\frac{\Delta \vec{x}}{\Delta y}=\frac{d\vec{x}}{dt}\]
When \(\Delta t\) approaches the zero the point \(R\) approaches point \(S\). In the limiting stage, the chord \(RS\) would become the tangent to the curve. The slope of this tangent would give the value of instantaneous velocity corresponding to the point \(S\).
If this tangent slopes towards the right then instantaneous velocity would be considered positive this is because of the positive value of the slope on the other hand if the tangent slopes downward to the right then the instantaneous velocity would be considered negative, because of the negative slope. If the tangent is parallel to the time axis then instantaneous velocity is zero